Уравнением линии на плоскости называется уравнение с двумя переменными 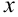 и
и 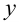 , которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Пример №6.1.
Определите, лежат ли точки 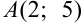 и
и 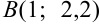 на линии, заданной уравнением
на линии, заданной уравнением 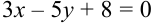 .
.
Решение:
Подставим в уравнение линии координаты точки  , получим:
, получим:
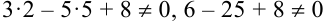
Следовательно, точка  не принадлежит заданной линии.
не принадлежит заданной линии.
Подставим в уравнение линии координаты точки 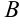 :
: 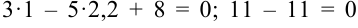 . Следовательно, точка
. Следовательно, точка 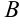 лежит на заданной линии.
лежит на заданной линии.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Координаты вектора на плоскости и в пространстве. |
| Операции над векторами в координатах. |
| Способы задания прямой. |
| Виды уравнений прямой. |

