Оглавление:

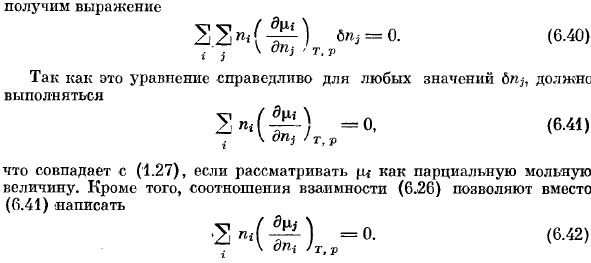



Уравнение Гиббса — Дюггема
- Уравнение Гиббса-Дюггема Выведено уравнение Гиббса ДУЕМА, связанное с приращением индифферентного химического потенциала.
Производная (6.24) равна、 (6.37) 6Г = 2 л <6Ш -} — г: Я… Если мы сравним это уравнение с (6.19)、 (6.38)) S6T-Vbp + Y = 0. Это уравнение является сосредоточенной переменной 7′, p, jii,…, cs включает вариации, а переменные расширения 6′, V, Hz необычны тем, что они являются коэффициентами перед ними.
Для изменений, происходящих при постоянной температуре и давлении(6.38), формула (6.39 ’) 6р. Т в ДНР нет.、 (6.39).)
Он связывает воедино изменения химического потенциала компонентов в изобарном изотермическом процессе. Людмила Фирмаль
В случае такого процесса (6.39)можно вычислить 6 из 1 (например, 6f. ii) (в других известных случаях). Если 6c *из (6.39) заменяется на значение Возвращает выражение SS ^ flT1) 6 ^ =0.(6.40)) 。 * Дж \ OUj, ти в Потому что это выражение допустимо для всех значений drij、 Улар-)= 0,(6.41) 。 \ drij JTyV если u рассматривается как частичная молярная величина, то она соответствует (1.27).Далее, по взаимосвязи(6.26), вместо (6.41), можно написать: Ч.
- Характеристики частичного молярного объема, рассмотренные в i,§ 3.It прекрасно применяется к химическим потенциалам. В случае двойного перемешивания, при котором молярная доля Х2 выбирается в качестве независимой переменной, ее можно описать следующим образом: Фюн Н ДСК дц2 п dtsg / оч _ = ——; -= —-(о. 4О.) dh2×2 демон oh2 Аналогично ДЦ н д И Д \ М дц2 Н дц2. -= —-; -= _-。 (о.44.) Почтовый индекс ox2 х [ЕП2 почтовый индекс ox2 Си ЕП2 (Индекс Tyr опущен здесь и в остальной части этого раздела.) «Это легко проверить (ср.(1.34)) ^ + ^ = 0. (6.45) dx2 dx2.
Для свободной энергии Гиббса Молле таким же образом, как и средний молярный объем (см. (1.35)), получаем следующее: е = = 2 * «и»; (6.46) 1 также относится к двоичным системам(ср.(1.36)) дециграмм. — =Р2-М1. (6.47))
Если мы дифференцируем (6.47) относительно x2, то получим: d2ë _ д ^ _ три пьесы с DXL dx2 dx2 £ 1 из производных здесь можно исключить с помощью (6.45). д [Кроме я \ / dхr、 +(6.48)) dx2 dx2 \ Си) £ Или ВПУ. — Сицзян’ dh2 \ ДХ ’ l, аналогичным образом д [оказывается _ Т
Уравнения (6.49)и (6.50) будут необходимы при обсуждении смещения вдоль линии равновесия. Людмила Фирмаль
Смотрите также:
| Фундаментальные теоремы | Химические потенциалы и производная дЛ/д£* |
| Термодинамические потенциалы как функции химических потенциалов | Многофазные системы |

