Оглавление:

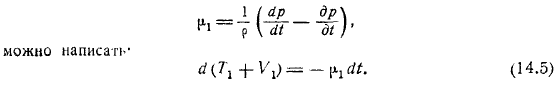

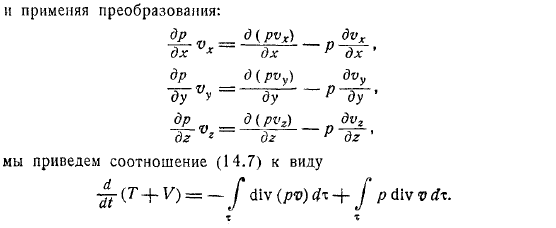



Уравнение энергии
Умножьте обе стороны уравнения на скаляр. Если поле внешних массовых сил неподвижно и сила имеет потенциал, то его можно назвать потенциальной энергией гидромеханики на единицу массы движущейся жидкости. Принимает следующий вид. Запоминание определения отдельных (полных) производных можно выразить в следующем виде.
Последнее уравнение является выражением закона биологических сил для единицы массы жидкости. Введение в нотацию. Ты можешь писать. Умножьте на основную массу и интегрируйте объем жидкости, окруженный замкнутой поверхностью. Поскольку мы рассматриваем объем переноса жидкости, состоящий из одних и тех же частиц, не зависит от времени и может быть описан следующим образом. Девятнадцатый век. Выражение. Ф-Техас.
Согласно этому закону, если вдоль линии потока давление жидкости возрастает, то скорость течения убывает, и наоборот. Людмила Фирмаль
Она представляет собой живую силу, или кинетическую энергию рассматриваемого объема жидкости.Вы можете назвать интеграл. Объем жидкости общая потенциальная энергия и —мера диссипативного объема. Вроде этого. Замените разницу через другой ОП. Применение преобразований. Приводит отношение к форме. Наконец, мы применяем преобразование Гаусса.
Отношение, где косинус угла, образованного внешней нормалью поверхности с координатными осями. Последнее уравнение называется уравнением энергии. Поверхность. Можно рассматривать как единицу времени работу поверхностных сил гидродинамического давления, приложенных к поверхности объема жидкости. Интеграл есть. Как указывает кинематика, расхождение закона количеств движения и закона моментов количеств движения между скоростями является относительным кубическим расширением жидкости, поэтому его можно считать работой внутренних сил, связанных с расширением каждого элемента объема.
Для несжимаемых жидкостей этот член в уравнении выпадает и уравнение энергии принимает вид. Кроме того, если объем жидкости окружен неподвижной границей, то вдоль нее. Тогда принимает вид уравнения равновесия. При таком объеме можно сделать вывод, что сумма кинетической и потенциальной энергий не изменяется со временем.
Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости (то есть без вязкости и теплопроводности). Людмила Фирмаль

