Оглавление:

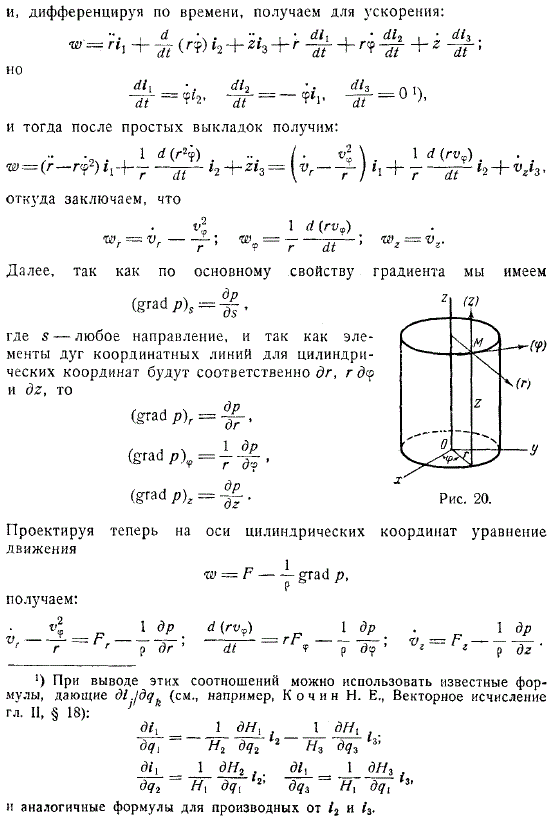

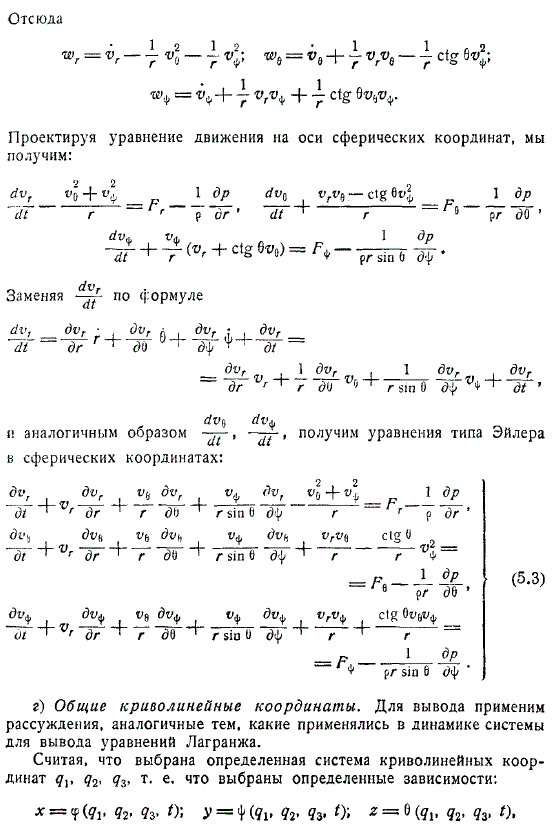



Уравнения движения и формула Эйлера
Уравнения движения Эйлера в виде декартовых координат. Уравнения Эйлера представляют собой проекции ускорения в переменной Эйлера в соответствии с этим разделом гидромеханики уравнения движения и решают уравнение так называемого уравнения гидродинамики Эйлера. Возвращает цилиндрические координаты. Проекция скорости точки на ось цилиндрических координат.
На что указывает кинематика точек.Отложив 3 единичных вектора вдоль оси цилиндрических координат, можно выразить вектор скорости точки в виде, и дифференцируя его во времени вы получите ускорение.
После простого вычисления вы получите кроме того, за счет основных свойств склона, где расположено любое направление, так как имеются, соответственно, элементы общего уравнения движения идеальной жидкости дуги координатной линии цилиндрических координат. Далее строятся уравнения движения по оси цилиндрических координат.
При выводе этих соотношений можно использовать известные формулы, такие как векторные вычисления и аналогичные формулы для производных названий этих уравнений, а также полные производные таким же образом мы достигаем типа дифференциальных уравнений Эйлера их подразделяют на:
- Сферические координаты
- Проекция скорости точки на ось сферы
Поместите вдоль оси сферические координаты единичных вектора
Представляют вектор скорости в некоторой точке в виде
Поэтому, для ускорения, вы получите следующее. Вы можете построить уравнения движения по оси сферы. Отсюда заменяйте формулу аналогично получаем уравнение Эйлера
в сферических координатах.
Общие криволинейные координаты;в заключение мы выводим уравнение Лагранжа, применяя выводы, аналогичные тем, которые используются в динамике системы. Предполагая, что выбрана определенная система криволинейных координат, выбирается определенная зависимость.
Построение уравнения движения
С другой стороны, при построении уравнения движения по оси сферических координат оно выглядит. Отсюда не заменяйте формулу аналогично получаем уравнение Эйлера в сферических координатах.
Общие криволинейные координаты;в заключение мы выводим уравнение Лагранжа, применяя выводы, аналогичные тем, которые используются в динамике системы.
Предполагая, что выбрана определенная криволинейная система координат, выбирается определенная зависимость. Сделать преобразование и когда применяется разбить на дроби.
Полные производные
То же самое верно и для других 2 терминов.Введение в нотацию рабочая сила на единицу массы жидкости и для обобщенных массовых сил найти уравнение движения и векторные формы уравнений движения в криволинейных координатах. Если есть потенциал в массовой силе, то очевидно и уравнения движения. Уравнения формы справедливы для криволинейных координат не только ортогональных.
| формула 1 | формула 2 | формула 3 |
| iL=-iI_l|L (j — 1, 2, 3) | iL=-iI_l|L (j — 5, 6, 7) | iL=-iI_l|L (j — 8, 9, 10) |
Проекция скорости на ось криволинейных координат представлена следующей формулой где же хромой фактор выглядит отрицательно.
В случае декартовой ортогональности биологические силы принимают вид положительных поэтому решение получается верным.

