Оглавление:




Уравнение Д. Бернулли для потока жидкости
Уравнение Д. Бернулли для потока жидкости. Рассмотрим поток жидкости (около 4.17) с плавно изменяющимся устойчивым движением. Выберите основную струйку с живым сечением iso и скоростью u. (4.56) энергия жидкости, протекающей через живое сечение элементарного потока、 де = yoyt(Р + +. 4—-) является постоянным и、 П81. Визуализация интегрального символа: Е = Ре(Р + М ^идея+ C и безопасным Согласно Лемме о 3 интегралах ^ iiso = rso и / и% & co = aP3co©© А потом поток энергии. Е = Р0-ЦУП ^ +% aY3 <о.
Для того чтобы энергия потока выражалась в единицах веса, а также элементарного потока, необходимо разделить каждый член уравнения на p ^ Kco, а удельная энергия потока равна E ^ a. * Р§UsoP8 + 28 Поперечные сечения 1-1 и 2-2 (rns.4.17), то есть если не считать потери энергии ex = ex-sop $ 1 от нее И \ 2§ 2% 4. » P2 4. И\ 2 е ’ (4 69) Формула (4.69) используется для определения течения стабильно и плавно изменяющейся невязкой жидкости (потери энергии не учитываются) по уравнению Д. Бернулли. 68.
Вы можете написать это так * + ^Р = const1. (4.70) При движении вязкой жидкости часть энергии потока расходуется на преодоление сопротивления между расчетными участками 1-1 и 2-2 (стенки потока и канала, силы трения возникают между частицами жидкости). в результате удельная энергия ex> e2 и последующих участков (направление движения) переносятся на предыдущую энергию (ex> e2>… в этом случае выражение (4.69) можно записать следующим образом.
Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Людмила Фирмаль
- Он рассчитывается для каждой единицы веса жидкости и рассчитывается относительно произвольно выбранной горизонтальной плоскости (опорной плоскости).Эта конкретная текучая энергия ■ П / aU2 е = р + я— 98 часов. + Где 2-удельный расход энергии на преодоление сопротивления между секциями 1-1 и 2-2. В общем случае формулу(4.71) можно записать с учетом потерь энергии k \ p между сечениями, рассчитанных в виде: + Ар = * как const *. (4.72) Формулы(4.71) и (4.72) относятся к D.
Уравнение д. Бернулли устанавливает связь между скоростью движения, давлением и геометрическим положением любой точки в Живом сечении потока, в котором оно записано. D. рассмотрим энергетическую и геометрическую интерпретацию (интерпретацию) уравнений Бернулли. D. энергетическая интерпретация уравнения Бернулли. С энергетической точки зрения уравнение Д. Бернулли представляет собой закон сохранения энергии и представляет собой определенную энергию.
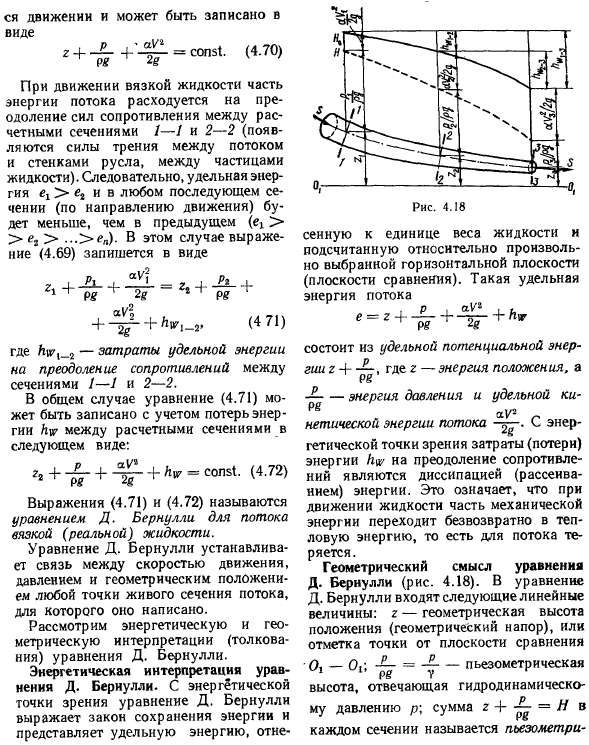
- Энергия давления и идентификация aU2 〜Эээ чистой энергии потока. С энергетической точки зрения затраты (потери) на преодоление сопротивления энергии/ gi / это диссипация (диссипация) энергии. Это означает, что при движении жидкости часть механической энергии безвозвратно преобразуется в тепловую. То есть она теряется из-за потока. D. геометрический смысл уравнения Бернулли(рис. 4.18).
Уравнение д. Бернулли содержит следующие линейные величины: r-высота геометрического положения (давление воздуха), или отметка точки от опорной плоскости ’0} Oh\•—пьезоэлектрическое измерение Высота соответствующее гидродинамическое давление P\сумма каждой секции Р + ■ = H называется пьезо метрических 69. Химическое (p = pIzb), или гидростатическое давление И Y2 Давление, скорость ^ 。 R aU2 и Давление; всего r + Гидродинамическое давление, или максимальное давление, называется и может быть выражено в уравнении.
Согласно (4.70), невязкая жидкость (за исключением потерь энергии) является горизонтальной. Когда вязкая жидкость движется, изменение давления в линии на единицу длины называется гидравлическим градиентом. Н0 = Н И V2 28 ’(4.73) Lg-потеря давления для преодоления сопротивления. Геометрическая точка сверху Конец отрезка суммы r + называется пьезометрической линией (обозначенной пунктирной линией на рис.4.18). Изменение пьезоэлектрического провода r +—•в длину блок называется пьезометрическим наклоном.
Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости. Людмила Фирмаль
- Длина пьезоэлектрического провода может стать короче Поскольку приращение dH0 всегда отрицательно(гидродинамическое давление уменьшается по ходу движения), гидравлический градиент всегда положителен. Средний гидравлический градиент 1: области между секциями (например, 1-1-2-2) могут быть представлены зависимостями. II < М * С II РГ 1» Я(-1 Л,< П&1 * е) ПЭ 1 2 * Увеличение. > 0.
Пьезометаллик Если пьезоэлектрический провод уменьшается с течением жидкости, то градиент считается положительным. Средний пьезоэлектрический градиент 1p в области между секциями (например, между 1-1 и 2-2) может быть выражен в виде зависимости. Геометрическое расположение точек верхнего a, p. a. aU2 Итого r + -{конец сегмента Она называется линией давления, или линией удельной энергии (рисунок 4.18 обозначен сплошной линией). (4.75) В общем случае уменьшение величины всего или части уравнения (4.73) может привести к потере давления.
Смотрите также:
Возможно эти страницы вам будут полезны:
Смотрите также:
Возможно эти страницы вам будут полезны:

