Оглавление:


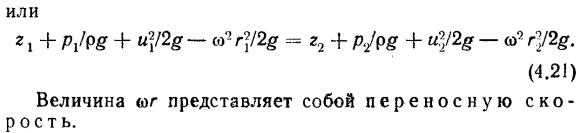

Уравнение Бернулли для частных случаев
Уравнение Бернулли для частных случаев. Применяя уравнение Бернулли (4.9) к фактическому расчету, необходимо определить вид потенциальной функции Р, зависящей от массовой силы, действующей на жидкость. 1.Масса, действующая на liquidgravity, является только 1.In в этом случае проекция на координатную ось распределения плотности массовых сил PX = RU = 0; Pr = §(ось 02 расположена вертикально вверх). 。(4.5 a)из этого дела ИС = §ИГ Или Н = ДГ + с(4.11).
Если скорость потока равна нулю, то энтальпия принимает максимальное значение. Людмила Фирмаль
- Полученное значение P подставляется в (4.9) ’для получения уравнения Бернулли стационарного движения несжимаемой невязкой жидкости под действием силы тяжести-1 масс.%г + п! п + А2 / 2 = СОП $ 1:(4.12) Или р + п / П8 + У2 /2§= сопи! (4.13) Для частиц в 2 положениях 1 и 2 уравнение Бернулли(4.12)и (4.13) можно записать в виде: § 1+ РХ / Р + «2/2 = 84 + / УР +» 1/2 (4.14) Или +РУР8 +2828 = ц + 22! § 98 +чу2. (4.15) 2.На жидкость действуют массовые силы: центробежная инерция силы тяжести, инерционное движение и инерция Кориолиса (в случае относительного движения).
- Такие движения наблюдаются, например, в криволинейных каналах, которые вращаются вокруг вертикальной оси с постоянной угловой скоростью (ω) (рис. 4.2). Выберите систему координат: прямая ось 84. 02 вдоль оси вращения поверните оси OX и OU вместе с каналом. Рассмотрим движение жидкости вдоль обтекаемой линии (или, что эквивалентно, основного потока жидкости). Пусть и-локальная скорость жидкости для выбранной вращающейся системы координат.
Гравитационная сила на единицу массы имеет проекцию. p * 1 = p1b=°; p ^ = ёЦентробежная сила инерции на единицу массы равна 2R (g-расстояние от оси вращения рассматриваемой точки). Ее проекция Pxg все = СО2 х; Py2 = СО2 г \ ПР2 = 0 Если вы думаете, что массовая сила имеет потенциал、 ИС = РХ х + ру уу + пиар-ый(4.16) И получить -Мп-автомат х-ых с? ю §ИГ. После интегрирования, находим П=-о*(х* +у’) / 2+§г+С. С тех пор G2 = X2 + y%, то = = § 2-СО2-Р2 / 2 + С.(4.17).
Расчеты, которые проводят для реальных жидкостей с применением уравнения Бернулли, дают неплохие результаты. Людмила Фирмаль
- Поскольку вектор силы Кориолиса перпендикулярен вектору относительной скорости жидкости, проекция не включает в себя прогнозируемое распределение плотности силы Кориолиса. Уравнение Бернулли рассматриваемого движения、 §+ п / п + У2 / 2-СО2 Р2 / 2 = сопи ((4.18) Или 2 + п! Р§+ u212§ СО2-Р2 /2§ константный (, (4.19) 2 секции элементарного потока включают+ Px / P +и\ 2-ω2г!2 =§ 2+ p2 / p + и!! 2-ω-г!2(4.20) 8 $ Или 21 + P ^ P0 + uY2o-M’R \12§= r2 + p2 / p§+и\!2§ А2 Р] /2§ (4.21) Размер Юга представляет мобильную скорость.
Смотрите также:
Возможно эти страницы вам будут полезны:
- Уравнения Громеки при действии массовых сил, имеющих потенциал.
- Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости при действии массовых сил, имеющих потенциал.
- Энергетическая интерпретация уравнения Бернулли для установившегося движения.
- Напряжения в движущейся вязкой жидкости.

