Оглавление:




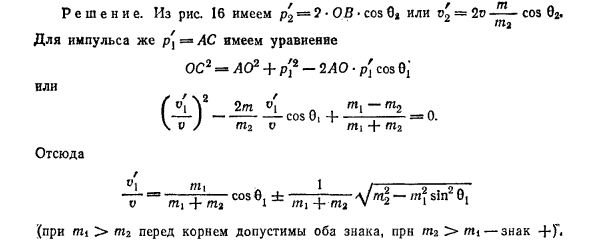

Упругие столкновения частиц в физике
- Упругое столкновение частиц Столкновение двух частиц иначе называется упругостью Сопутствующие изменения во внутреннем состоянии Поэтому при применении законов сохранения энергии к таким столкновениям внутреннюю энергию частиц можно игнорировать.
Самое простое столкновение — система отсчета (система c), где центр инерции обеих частиц неподвижен. Как и в предыдущем разделе, мы дифференцируем количественные значения в этой системе по индексу 0. Скорость частиц до столкновения в c-системе связана со скоростями vi и v2 в лабораторной системе в зависимости от соотношения. 777-2 777/1 V10 = 7-7-1-1-Н — 7-7-7-2-2 В> v 20 = — 7-77 — / — 1 — + — G-P-2 V> Где v = vi-v2 (см. (13.2)).
импульса обеих частиц Величины столкновений остаются неизменными Людмила Фирмаль
Согласно закону сохранения импульса,, а направления остаются противоположными, а их абсолютные значения не меняются в силу закона сохранения энергии. Таким образом, результат столкновения уменьшается в системе c, что приводит к вращению обеих скоростей частиц.
Эти частицы остаются противоположными по размеру. Выражается в виде единичного вектора в направлении скорости частицы m \ после столкновения, скорости обеих частиц после столкновения ( Буду лизать их ударом) 1 777/2 1 _ 777/1 (L * «7 1 \ Vi n = ——— ga1o, Von = ———— ga1o. (17.1) iU 777/1 + 777/2 ^ GHZ + GP2 V ‘ Чтобы вернуться к лабораторной системе отсчета, Добавьте центр инерционной скорости V к этим уравнениям.
- Следовательно, скорость частиц l-системы после столкновения следующая. 1 1712, 777 / 1В 1 + 777-2 В 2 vi = — r> n0 H ——— ——-, 777/1 “b 777-2 ГГц + 777/2 (1 7 * 2) 1 1711, 1711 В I + TP2 V 2 » ‘ v2 = ——-— vuq H —————. 777/1 + 7712 7771 + 7772 Это исчерпывает доступную информацию Столкновение основано только на законе сохранения импульса и энергии.
Для направления вдоль вектора, Зависит от закона взаимодействия частиц и относительного положения частицы при ударе. Результат может быть интерпретирован геометрией Чески. Удобнее переключаться со скорости на пульс. Умножая уравнение (17.2) на m \ и m2 соответственно, получим: pi = m vnоЧ —— ^ — (piЧ-prg), 777/1 + 1712 (17 ° С) е, 7722 /, \ p * = — «1, n» + ^ m ^ (p 1+ p2) (Ha = GP1GP2 / (rai + ha2) — потеря массы).
Если единичный вектор ориентирован вдоль Людмила Фирмаль
Давайте сделаем Создает то, что показано на рисунке с радиусом mv. 15 сборок. ОС, вектор AS l CB дает импульсы p’x и p ^ соответственно. при Пи и П2 радиус окружности и местоположение точки Точка C может быть размещена в любом месте круга.
Одна из частиц (пусть Частица м2) до тех пор, пока не прекратится столкновение. В этом случае = VO anild2171-pi = mv соответствует радиусу. Точка B 171! + 1712 Это на круге. Вектор AB соответствует импульсу pi. Первая частица перед рассеянием. В этом случае точка А находится внутри (Если mi m2).
Соответствующий рисунок показан на рисунке. 16 а и б. Показанные на них углы 01 и 02 являются углами отклонения частиц. и OS = mv] рай (пи + р2). ми <м2 АО = OB = ми + м2 м2 (пирог + P 2) AB = пи; АО j OB = ми / м2 ми + м2 Рис. 15 Рис. 16 После столкновения в направлении столкновения Доска пи). Центральный угол, обозначенный x (направление направления) на фигуре, представляет угол поворота первой частицы инерциальной системы.
С рисунка Очевидно, что углы 01 и 02 могут быть представлены углом x. официальный = rn2 sinx 02 = (17> 4) t 1 + m2 cosx 2 Также запишите формулу, которая определяет абсолютную величину скорости обеих частиц после прохождения через одну и ту же частицу Угол х: vi = y / m \ + m \ + 2 w x w 2 c o s x ми + м2 v2 = 2miv я + 777-2 в преступление 2 (17,5) Total 01 + 02 — угол рассеивания частиц после столкновения.
Очевидно, 01 + 02> тг / 2 для ми <м2, 0i + 02 <тг / 2 для ми ми> м2 • Когда обе частицы движутся после столкновения Вдоль прямой линии («лобовое столкновение»), соответствующей x- ^ Расположение точки С на левом диаметре точки А (рис. В этом случае Pi и P2 противоположны друг другу) или между A и O (На рисунке? ‘? B \’, p’x и p * 2 в одном направлении).
В этом случае скорости частиц после столкновения равны. Vr mr-m 2 1 2 m i (l * 7 a \ i = ——— v, Vo = ———- v. (17.6) m i + w 2 m i + w 2 Значение v2 является максимально возможным. Следовательно, максимальная энергия, которую первая стационарная частица может получить в результате столкновения, равна T7if ^ 2 ^ 2 m a x 4 7 7 li 777-2 tr (L 1) — ^ 2max = -j- = (Ш1 + Ш2) 2Åб (17-7) 1-1 777-117? Где bi = —— — начальная энергия падающей частицы.
Если mi m2, угол отклонения летящей частицы не может превышать некоторый максимум, соответствующий положению этой точки C. (Рисунок ?? 5), прямая АСЛ {~ Коснитесь круга. Очевидно, что sin0imax = OS / OA или грех 01 проверка = — • (17,8) Ш1 Рис. 17 Особенно похоже на столкновение Образование частиц с одинаковой массой (сначала это стационарно).
В этом случае не только точка B, Точка А находится на окружности (рисунок 17). В то же время 01 = |, 02 = ^, (17,9) v [= vcos ^ vf2 = vsm ^. (17.10) Обратите внимание, что частицы после удара рассеиваются под прямым углом друг к другу. После столкновения заданной движущейся частицы (mi) и неподвижной частицы (m2) выразите скорость обеих частиц через угол отклонения системы l. 777 / Решения.
С рисунка? p’2 = 2-OS-cos02 или v’2 = 2v —- cos 02- м2 Если импульс p1 = AC, уравнение OS2 = AO2 + p 2-2AOpi cos0i или 2 2t v [ Отсюда VI В VI В ми , Ми-м2 cos 0i N ————— м2 v т 1 + м2 0. cos 0i d = m \ -mn \ sin2 0i ми + м2 ми + м2 (Если mi> m2, вы можете использовать оба символа перед маршрутом; если m2> mi, вы можете использовать символ +).
Смотрите также:
| Кеплерова задача | Рассеяние частиц в физике |
| Распад частиц в физике | Формула Резерфорда |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

