Оглавление:















Универсальное уравнение оси изогнутого бруса (метод начальных параметров)
- Универсальное уравнение для криволинейной оси Балки(метод начальных параметров) Задача определения прогиба решается путем применения так называемого универсального уравнения оси криволинейной балки, или, как часто говорят, вывода универсального уравнения упругой линии, основанного на так называемом методе начального параметра, который широко используется в строительной механике. Таким образом 279прогиб любого сечения балки определяется коэффициентами смещения и силы, принятыми в начале координат, с учетом нагрузки,
приложенной к балке. Представим себе, что на балку действует любая система нагрузок. 248, а. Интенсивность нагрузки и концентрированный ТАТ при этом совпадают с направлением оси ОП, которая направлена вверх. Внешний сосредоточенный момент положителен при действии по часовой стрелке. Начало координат совместимо с центроидом секции в дальнем левом углу луча. Жесткость балки считается определенной длиной. Для каждой секции разделите несколько секций за один раз так, чтобы изгибающий момент был представлен непрерывной функцией
Сила давайте щи-положительная, что направление Все ее балки на полу на растяжке — Людмила Фирмаль
— о- • • Граничная точка/, 2,… Кроме того, разделительная секция должна быть размещена в тех секциях, где происходит изменение закона балансировки нагрузки. Так, например, происходит переход к закону нагрузки a<7 или ее распределению изменений, применяется концентрированный момент, и применяется переход к графику момента A/I=M1. Давайте сначала рассмотрим первый раздел 280 кватиум, для которого согласно(9.5) дифференциальное уравнение имеет вид M1m здесь-отклонение любого участка первого участка./ I1 представляет собой значение изгибающего момента любого участка первой секции Разложите отклоняющую функцию на(0)+
(0)I+SG(0)+V(0)ряд Маклорина. (б) в этом уравнении, размер G?Значения функций A1(x) и ее производных, таких как 1(0), y'(0) и SG (0), находятся в начале координат, то есть x=0. Запишите различия зависимостей: (IV _ СЛР _ м 4) 5~ ~ ~ ET’ 1SRA_1(1М.(1x3E^YH_1L? _ с/h4e по^<1х~Э~ ‘с/5o_1L/с/X5E/з / ч’ С дальнейшей дифференциацией, мы имеем с(lo_1(1П~1Д/с хорошо.у~ых^~ ~ эз АХА~—’*■» Поставим X = 0, обозначив следующее: V^(0)=u0 и(0) = Fo-угол отклонения и поворота в начале координат;M1(0)=M0 и(0)=F0-момент o сечения, взятого в начале координат » — это сила нагрузки, взятой в начале координат, и ее производные, т. е. x=0. Затем, основываясь на дифференциальной зависимости (C)между коэффициентами ряда Маклорина (b) и
- принятой нотацией, получаем следующее уравнение:m°)=»®;. O1 (0) = Fo; = &7<°) = «^7» ‘ 281 «у»(0) — * ; (0) — . . . Если присвоить эти значения в выражение (б), вы получаете 4 » Fo * +■<2O X3I^0X*I21G E / 3! Е4 4! . ЯО X5 Яо XW +-Например»5! g~ET~BG+(9.6)полученное выражение может выражать прогиб в любом сечении первого сечения через начальные параметры u0, C?0, МО… Некоторые из этих параметров известны заранее, некоторые определяются из граничных условий. Чтобы получить уравнение отклонения оси балки во втором сечении, выполните следующие действия: По формуле, полученной для первого участка (9.6), строим кривую в двух участках-первом и втором. Во время первого раздела (рис. Пунктирная линия-248, г) она представлена толстой линией, проходящей через второе сечение.
Пунктирная линия-это изображение линии, описываемой формулой (9.6), но она не соответствует истинной кривой криволинейной оси луча второй части, нарисованной толстой линией. Координаты между двумя кривыми заштрихованы на чертеже. Аналитически эти координаты представляются уравнениями Ду (х)=ду=у,—у,. (d)определяем величину du, затем находим отклонение луча во втором сечении: Координирует =у 4-Ду. (e)для этой цели мы пишем два дифференциальных уравнения: y2o, M, 42, M, «LX2= — E7 — ‘» Ix2 » = — E7 — *при вычитании первого уравнения из второго、 Показ был ДМ,=М» — М ,, 4″, DM, AH2~ ~ ЕГ~*(е)
Исходя из сходства дифференциального уравнения 282 (e) с основным уравнением(a), можно утверждать, что решение функции Du совпадает с решением, полученным для функции Людмила Фирмаль
(9.6). В этом решении вместо координаты x нам нужно взять координаты, которые отсчитываются от точки 7, а именно (x-P1). Вместо значения M o -, <20; D0… И так далее. Следует принимать DL4,; D<2G, D<71;… И так далее. Следовательно, Ду=Ду, 4-дер, (х-а) 4-2!°1) 2+D<21+ Ми^ Л?Один. Иезекииль. (х-^U41 Ди?; ЕС (ч-к ao5 , 5! +(9.7) Где Du,=Du, (x) — функция, определяемая равенством(g) в следующем разделе(рис. 248, г); Ду — переход на линию прогиба точки 7;д<р-прыгать, чтобы угол поворота точки 7; d7y, — перейти к сюжету момент точки 7, 246, б). Это значение равно внешнему сосредоточенному моменту, приложенному в данной точке. 248, в), равная внешней сосредоточенной силе, приложенной в точке 7; D<7! —
Скачок силы нагрузки в точке 7; D<7, — скачок дифференциации силы нагрузки в точке 7; Все значения прыжка, перечисленные здесь, определяются как разница между двумя значениями соответствующих значений, взятых в точке 7. Например, Ди?1=[<7Р М-Я, (•»)]»…. (9.8)где^,,, (x)и<7,(x) — функция, определяющая закон изменения распределенной нагрузки второй и первой секции. Значение ‘D^’ определяется как разность между производными.»d<71’=[d’p (x) — I(x)]x=Y1= ®2 — «1- (9.9) где А2 и а — угол наклона касательной к эпюре
нагрузки, взятой в точке 7 (см. Рисунок). 248, а). Если шарнир расположен в точке 1, то может произойти скачок угла поворота, поэтому левый и правый углы поворота точки 1 различны(см. фиг. 249, а). Как показано на рисунке, скачок отклонения возможен, если балка в точке 1 разрезана на две части, соединенные параллельными стержнями. 249, b. результатом является два отклонения луча.hke1 отличаются друг от друга, как показано на диаграмме отклонения(рис. 249, в). Для сплошных балок, не имеющих разрезов по всей длине или полных швов, в том числе при/,=0. +А»! +(Д! Я+Л Г П);}(Ш) с-1…………………………………………………| ИНТЕЛЛЕКТУАЛЬНАЯ
СОБСТВЕННОСТЬ= +2 / =1 И в то же время, используя уравнения (9.6) и (9.7), получаем универсальное уравнение прогиба любого сечения 1=1 1=1 1! L40x2 О Х3 п — +ФО * +е Д2! +Е}3! 1<7o|1 4! + Л-1л-1 Е7 5! f’dfdh -^) + / -1 / =1 с-1 У ДМ, +5 — (х -/) 3,3! «• Я в(Х, г(х-^Г2;е/41g5 / 5! Г <=1/=1 (9.10)) Дифференцируя, мы получаем универсальное уравнение для угла поворота 284: При решении конкретной задачи некоторые члены, содержащиеся в уравнениях (9.10) и (9.11), равны нулю. Полученные уравнения(9.10) и (9.11) зависят от значений O0;Fo’, M o;f0;D’o и др. Метод решения этих уравнений называется методом начальных параметров. Все исходные параметры, некоторые параметры
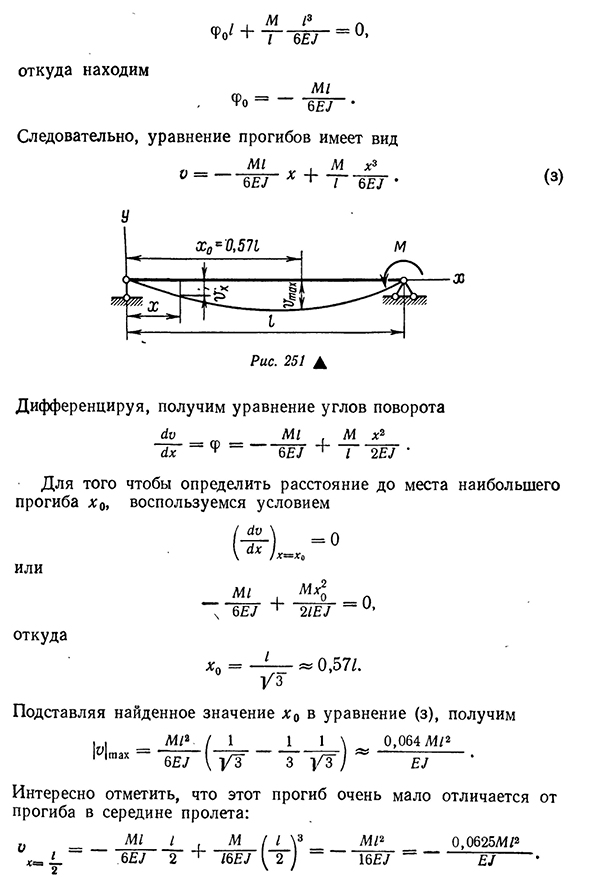
известны. Обычно для условия задачи задаются значения<70 и D0n. M0 и F0, из условий статики, и если задача статически неопределима, должны быть известны или определены из условий деформации. Значения o и f0 не могут быть определены из условия статического равновесия. Определение этих начальных параметров производится по граничным условиям. Так, например, о балке, которая показана на схеме. 250, a, 0 и 1__ 1 _ \ 6 е/\у z3u з ) 0. 064M12 Е } Интересно, что этот прогиб мало отличается от прогиба в середине пролета: «M1I, M/I\3_M12 0, 0625L4 / 2 2+/6Е/компания i2i~16EU~Е7 Два» 287П Р и М Е Р2. Напишите уравнение отклонения луча и угла поворота, показанного на рисунке. 252, определение максимального отклонения. Путем устанавливать начало на уплотнении, мы имеем: =0;Фо= ++ Два. Один.
Два. 6″ (^1 + «4» ^2 ] = — 32 T * m; В первом разделе по формуле (9.10) получаем уравнение прогиба Я Я^02И Ф О Х3 Ч — «о+F0h+-е-2г+и Г» ЗГ+• * = 32×2 10X3~E / 2+E / 6′ Эта формула действительна, если два участка примыкают к точке 1:на первом участке точки/<7=0, на втором участке той же точки<7=—<7. При переходе с первого сайта на второй сайт/через точку он изменяется от 0 до-<7. Таким образом, D<7X= — <7^, чтобы избежать ошибок в определении размера и знака D_ Е^6E7 2 (x-2)4 24 3 (x-2) b EU120 Уравнение угла поворота и отклонения:первая секция (/В С дифференциацией.— Тридцать два. Икс Е. Один Десять. T7 X2 + Для второй части х+у Х2 2(х-2)3Е]6 Наибольшим прогибом
второго становится правый край левого x= / = 4m в уравнении прогиба второго участка получаем Два, два, два, два, два, два ^tah15E7 Знак минус указывает на то, что отклонение не совпадает с осью операционного усилителя(на выходе ось операционного усилителя положительна). В растворе размеры балки измеряются в метрах, а нагрузка осуществляется в тоннах на погонный метр.、- Из базы- Рис 253А 28$маскирует его, и вы должны занять на Gives / m2 и M4. В результате мы получаем отклонение в метрах. П р и М Е Р3. Напишите уравнение отклонения луча, показанное на рисунке. 253, а, и определить прогиб в середине пролета. Начальные параметры этой задачи: Sh=0; Fo= / = O; Mo=0; Два. В полученном уравнении отклонения
значение CP0 неизвестно. Для его определения мы используем условие, что отклонение правой опоры равно нулю; так как правая опора принадлежит второй секции, а затем второй секции. GP ,, / П, Д1\I3P I3Dr п — ФО.»4 — ^ 2 4- 8 48 24- когда мы решаем это уравнение для 16EU-CP0、 P / 2 4) 0 » 16E/ 7d13 384E7 * Подставляя значение CP0 в уравнение отклонения, мы, наконец, получаем:теперь мы находим отклонение в середине пролета. Если вы поместите x= — y в первое уравнение, это выглядит так Rrddr^=2 — «» 48E7 768EU • Это значение также может быть определено из второго уравнения, так как середина пролета относится ко второму участку. Легко заметить, что последние два
члена второго уравнения X=-y исчезают, поэтому мы получаем тот же результат. Если в этой задаче поставить d=0, то произойдет отклонение луча от концентрации в середине пролета (рис. 253, б) Р-Р АТО. И угол поворота поддержки Р-Р Рис 254А П р и М Е Р4. Для риса. 254, и показана система, состоящая из двух балок,соединенных стяжкой, которая допускает свободное взаимное перемещение в направлении, перпендикулярном оси балки соединения, но только.Вы хотите построить линию отклонения. Эта задача является более сложной, чем предыдущие три задачи. Во-первых, найти ответ поддержки. Для этого мысленно соедините две части луча, отсоедините соединение и рассмотрите равновесие правой части. Легко установить, что опорная реакция правильной опоры равна
нулю. Тогда легко определить реакцию и момент в уплотнении, который показан на рисунке. 254, авг.Начальные параметры в уплотнении с началом координат следующие: А0=0;М0= — 8Т-м \ Фо=О’^О — ‘ в точке 1, Д(Д= — 4Т.Точка 2TO2=^=0. Применяя универсальное уравнение(9.10), получаем: о первом разделе 2 5 / + 6 5 / ‘ 0 < x<2; (и) Вторая часть РА 8 х 2-25 / 4 x 3 4(h-2)3+»6E7 6 5/(K) Для третьего раздела 8 × 2-й / 4×365? 4 (x-2)3 6 5 / Четыре. В последнем уравнении значение DU2 неизвестно. Для его определения используется условие, равное нулевому отклонению точки 3. Поставим X=8 и уравняем уравнение отклонения третьего сечения до нуля, получим 8 82 | 4-83 4-63 да. 2 ‘e. G’ (мм «g»~ Где его найти Сто семьдесят шесть 3 5 / * Поэтому формула отклонения третьего участка принимает вид 8х2. 4×3-4 (x-2) 3. 1 7 6. . . В H1— 2 5 / 6 5 / 6 5 / 35/ ‘ (л ) Интересно, что балки секций 1-2 и 2-3, все секции балки этих двух секций потому что реакция правой опоры равна нулю это говорит о том, что УР падает на
Смотрите также:

