Оглавление:
Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными 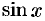 и
и 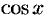 , над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать
, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать 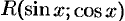 , где
, где 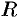 — знак рациональной функции.
— знак рациональной функции.
Вычисление неопределенных интегралов типа 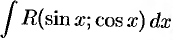
сводится к вычислению интегралов от рациональной функции подстановкой 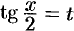 , которая называется универсальной.
, которая называется универсальной.
Действительно, 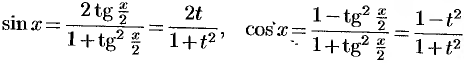 ,
, 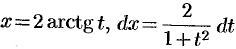 . Поэтому
. Поэтому
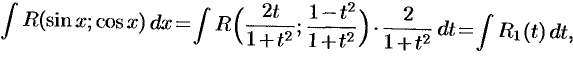
где 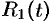 — рациональная функция от
— рациональная функция от  . Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.
. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.
На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной функции. В частности, удобны следующие правила:
1) если функция 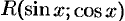 нечетна относительно
нечетна относительно 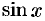 , т. е.
, т. е. 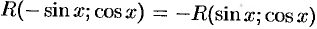 , то подстановка
, то подстановка 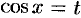 рационализирует интеграл;
рационализирует интеграл;
2) если функция 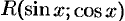 нечетна относительно
нечетна относительно 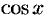 , т. е.
, т. е.  , то делается подстановка
, то делается подстановка 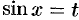 ;
;
3) если функция 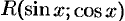 четна относительно
четна относительно 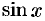 и
и 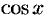
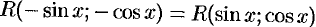 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 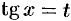 . Такая же подстановка применяется, если интеграл имеет вид
. Такая же подстановка применяется, если интеграл имеет вид 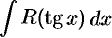 .
.
Пример №32.1.
Найти интеграл 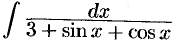 .
.
Решение:
Сделаем универсальную подстановку 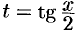 . Тогда
. Тогда 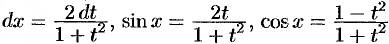 . Следовательно,
. Следовательно,
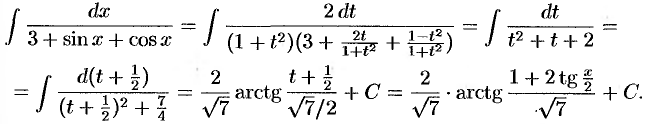
Дополнительный пример №32.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дробно-рациональная функция |
| Интегрирование рациональных дробей |
| Интегралы типа sin m x cos n x dx |
| Использование тригонометрических преобразований |

