Оглавление:
Умножение на сопряжённое выражение
Назовём выражение А , зависящее от одной или нескольких переменных (и тождественно не равное нулю), сопряжённым к выражению В, содержащему модули, если произведение АВ не содержит модулей.
Например, выражение вида 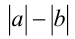 является сопряжённым к выражению
является сопряжённым к выражению 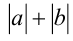 , и наоборот, выражение
, и наоборот, выражение 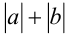 является сопряжённым к выражению
является сопряжённым к выражению 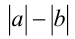 , поскольку их произведение
, поскольку их произведение 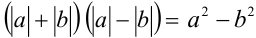 не содержит модулей. Рассмотрим пример, где приём умножения на сопряженное выражение (в указанном выше смысле) позволяет существенно упростить решение задачи.
не содержит модулей. Рассмотрим пример, где приём умножения на сопряженное выражение (в указанном выше смысле) позволяет существенно упростить решение задачи.
Пример №277.
Решить неравенство
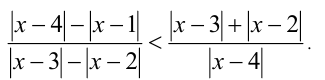
Решение:
Поищем более эффективный способ решения, чем стандартный метод интервалов. Умножим неравенство на положительное выражение 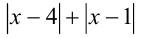 (сопряжённое к числителю левой дроби), и одновременно поделим неравенство на положительное выражение
(сопряжённое к числителю левой дроби), и одновременно поделим неравенство на положительное выражение 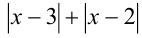 (сопряжённое к знаменателю левой дроби). В результате не только исчезнут все модули в левой части неравенства, но и, в результате сокращения на
(сопряжённое к знаменателю левой дроби). В результате не только исчезнут все модули в левой части неравенства, но и, в результате сокращения на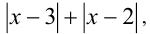 упростится правая часть:
упростится правая часть:
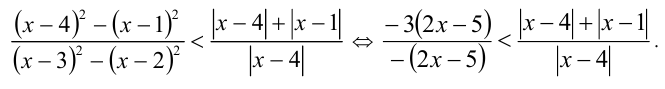
Последнее неравенство равносильно системе
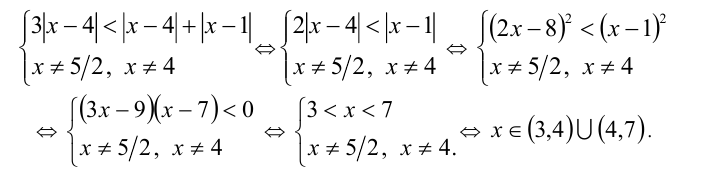
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

