Оглавление:
Умножение на функцию
Этот приём используют иногда в преобразованиях, например, с целью свести к известной формуле сокращённого умножения или избавиться от иррациональности (домножение на сопряжённое выражение). Важно при этом анализировать, сохранится ли в результате такого домножения множество решений задачи, не допустить потери корней и отследить возникновение посторонних решений.
При решении неравенств обычно приходится следить за равносильностью преобразований неравенства на его ОДЗ, и поэтому можно умножать обе
части неравенства на функцию, принимающую на ОДЗ неравенства только значения одного знака, либо разбивать ОДЗ на промежутки, на которых функция знакопостоянна, и делать равносильные преобразования на этих промежутках.
Пример №370.
Решить уравнение 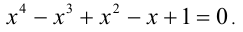
Решение:
Умножим обе части уравнения на 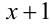 :
:
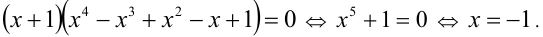
Заметим, что при умножении уравнения на 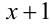 был приобретён посторонний корень
был приобретён посторонний корень 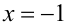 (это показывает проверка, которую сделать необходимо). Ответ: уравнение не имеет решений.
(это показывает проверка, которую сделать необходимо). Ответ: уравнение не имеет решений.
Пример №371.
Решить уравнение 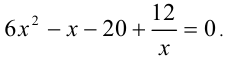
Решение:
ОДЗ: 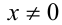 . Умножим обе части данного уравнения на выражение
. Умножим обе части данного уравнения на выражение 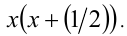 Получаем уравнение-следствие:
Получаем уравнение-следствие:
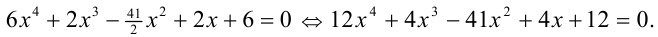
Данное уравнение является симметрическим уравнением 4-й степени. Решим его. Для этого разделим обе части уравнения на 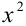 :
:
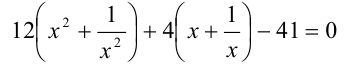
и сделаем замену 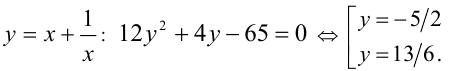
Тогда имеем совокупность уравнений
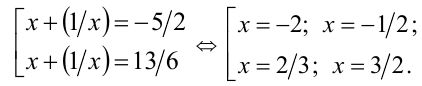
Легко проверить, что 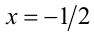 не удовлетворяет исходному уравнению, это посторонний корень. Ответ:
не удовлетворяет исходному уравнению, это посторонний корень. Ответ: 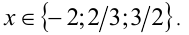
Рассмотрим некоторые из нестандартных методов, применяемых для решения математических задач. Именно знание этих методов и умение воспользоваться ими в подходящей ситуации отличает хорошо подготовленного абитуриента от абитуриента со стандартным базовым набором знаний классических и хорошо известных приёмов. Многие из методов, рассмотренных ниже, основаны на таких свойствах функций, как ограниченность, монотонность, обратимость 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

