Оглавление:
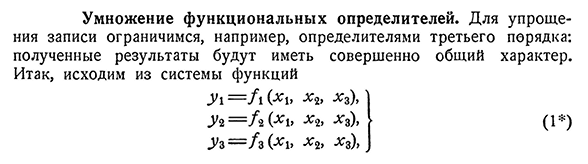



Умножение функциональных определителей
- Умножение функциональных детерминант. Для упрощения записей ограничимся, например, определителем третьего порядка: полученный результат будет иметь абсолютно общий характер. Итак,
исходим из системы функций U1=/1 (1>х г, Х3), _u2=а (Х1, ХГ, Х3),. УЗ-/З О Б Х3), (1) 208CHAP. Неявная функция. Функциональные детерминанты[325] Он определяется в (трехмерной) области
и имеет непрерывную частную производную для всех переменных. Людмила Фирмаль
Кроме системы функций (1*), возьмем систему функций Х1-^2, * З),^2=?2 (*Б^2>^з)> * з=? зо’л, ч), (2) И наличие непрерывной производной в (трехмерной) области гарантирует, что соответствующая точка (x b x2, x3) не покидает область (1B в et5 изменяется на y%, а затем
умножает функциональный детерминант системы (1).*) Дух-дю — ^духа д НД д x2du2du2du2du^д x1d x2d x3d по u3du3du3d X1D x2d Х3 О функциональных детерминантах системы(2) Д х г ДХ±D х 1-х D12d13d 2dx2w D12d13d х 3D х 3D 3D12d13 В этом случае мы используем
- известную теорему умножения детерминант, которая выражается формулой СК C12C13C2 1#22C23 # 31#32 # 33 Куда? ^11^12^13 ^21^22^23 ^31^32^33 а п ^21^22^23 # 31#32 # 33 (/, 6 = 1 , 2, 3) (Умножается на «строка по столбцу»). В нашем случае < > ДХ^в 1К _ DU1. делать;дг1 бы x2d Х2 1до\д * K1d Х3 д Х3 А именно-формула производной комплексной функции-326]§3. Определение функции 209 Наконец,
результат является определяющим фактором dU1 spirit$U1d^z DU2DI2DU2D11D1A d13 > du3gu8d8 И это функциональный детерминант системы функций u u Uz в переменных 1 и 1%. Итак, в простой нотации: В (ООН г%>УЗ)=в(.U1ch у^ч УЖД)в(x1U Х2,в непосредственной близости от отеля) В(А,Г2, 13)О (*!, x2, x3) и(^ , *2, 13) * 1 7 Если бы мы имели функцию y от x, то x была бы функцией переменной I, а для производной комплексной функции она имела
бы обычный вид (1U (IV (1x))):; Формула (3) была бы для нее одинаковой. Людмила Фирмаль
Обратим особое внимание, если переменная идентична Y & Y, так как система функций(2)является результатом»I и I» системы (1) (здесь приведенное выше соотношение таких обращений будет: В(U и U2ch УЖД). V(х р х2, х3) ІТ в(Х р Х2,Х8) ‘ О(у У2,У3) К7 Или В(ч>U2h УЗ)_ } в (Х р Х2,%З) в (ХР х2,а бизнес) V (до У2,УЗ) В таком виде она напоминает формулу производной обратной функции.
Смотрите также:
Решение задач по математическому анализу

