Если даны две плоскости, заданные общими уравнениями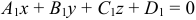 
и 
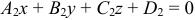, то определение угла между указанными плоскостями сводится к определению угла 
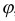между их нормальными векторам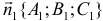и 
и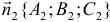 
. Из определения скалярного произведения следует
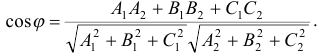
Тогда условие параллельности двух плоскостей эквивалентно условию коллинеарности нормальных векторов этих плоскостей. По определению два вектора коллинеарны, если их компоненты пропорциональны:
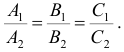
Условие перпендикулярности двух плоскостей:
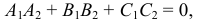
т.е. равенство нулю скалярного произведения нормальных векторов.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Определение угла между прямыми |
| Различные виды уравнения плоскости |
| Прямая линия в пространстве |
| Кривые второго порядка: эллипс, гипербола, парабола |
