Оглавление:
Угол и конус трения
Представим себе тело, опирающееся на шероховатую поверхность (рис. 73). Если бы поверхность была абсолютно гладкой, то она представляла бы собой идеальную связь, действие которой на тело сводилось бы, как мы знаем, к одной лишь нормальной реакции. Если же опорная поверхность—шероховатая, то при наличии силы, стремящейся сдвинуть тело, появится еще сила трения, лежащая в касательной плоскости и направленная в сторону, противоположную той, в которую мы движем или пытаемся сдвинуть тело. Если мы будем рассматривать критический момент (когда тело будет находиться, так сказать, на грани между покоем и движением), то для этого случая сила трения будет иметь максимальное значение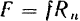 
. Две составляющие реакции: нормальная 
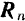и касательная (сила трения) 
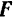, складываясь по правилу параллелограмма, дадут полную реакцию 
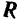опорной поверхности, которая теперь будет уже составлять некоторый угол 
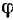с нормалью к этой поверхности.
Наибольший угол 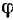, на который вследствие трения отклоняется от нормали реакция 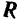шероховатой поверхности, называется углом трения.
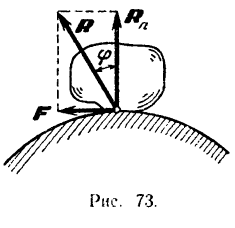
Из рис. 73 имеем:
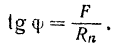
Но, как это видно из формулы (31),
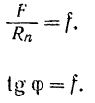
Тангенс угла трения равен коэффициенту трения скольжения.
Если мы рассматриваем тело, имеющее возможность перемещаться по шероховатой опорной поверхности в любом направлении, то линии действия возможных реакций 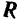этой поверхности образуют (рис. 74) коническую поверхность.
Конус, образующие которого наклонены под углом трения 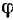к нормали к поверхности скольжения в данной точке, называется конусом трения.
Если коэффициент трения при движении тела в различных направлениях по данной поверхности одинаков, то полная реакция этой поверхности отклоняется от нормали во всех направлениях на одинаковый угол трения 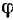, и конус трения будет круглым с углом раствора 
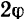. Если же, как иногда бывает (например, при трении по дереву вдоль и поперек волокон), коэффициент трения при движении тела в разных направлениях имеет различные значения, то конус трения будет некруглым.
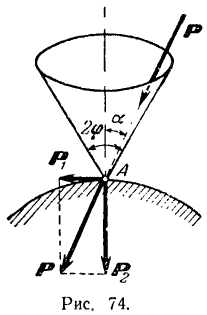
Пусть действующие на тело силы приводятся к одной равнодействующей силе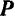 
, проходящей через точку касания тела с поверхностью и образующей с нормалью к поверхности в этой точке угол 
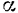(рис. 74). Перенесем эту силу по линии ее действия в точку 
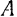и разложим ее на две составляющие: 
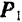, лежащую в касательной плоскости, и 
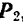, направленную по нормали к поверхности. Тогда согласно формулам (31) и (32) максимальное значение силы трения покоя будет
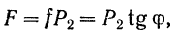
где 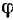— угол трения, а 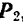— модуль силы нормального давления тела на поверхность.
Модуль же силы 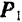стремящейся заставить скользить тело по поверхности, будет
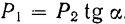
Для того чтобы тело оставалось на поверхности в равновесии, необходимо соблюдение условия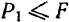 
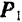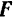или, если подставить значения и в это неравенство, 
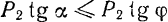. Отсюда получаем, что условием равновесия тела на поверхности будет
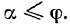
Если мы будем увеличивать модуль силы 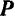, оставляя неизменным ее направление, то пропорционально будет увеличиваться не только модуль 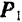движущей силы, но и модуль 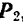силы нормального давления, а это неизбежно влечет за собой и соответствующее увеличение силы трения, и тело по-прежнему будет оставаться в равновесии. Этим объясняются известные из практики явления заклинивания или самоторможения тел. Тело придет в движение лишь тогда, когда модуль силы 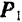сделается больше, модуля силы 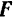, а для этого нужно изменить направление силы 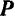так, чтобы угол ос сделался больше угла трения 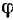, т. е. чтобы сила 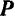проходила вне конуса трения. Следовательно, если равнодействующая 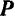всех сил, приложенных к телу, каков бы ни был ее модуль, проходит внутри конуса трения, то тело остается в покос, возникновение движения возможно лишь в том случае, когда эта равнодействующая проходит вне конуса трения. Этим замечательным свойством области, заключенной внутри конуса трения, и вызвано его название.
Пример задачи:
Плоскость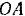 
(рис. 75) вращается на шарнире 
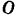так, что ее можно установить, под любым углом к горизонту. На эту плоскость положено тело 
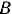весом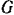 
. При каком наибольшем угле 
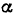наклона плоскости тело будет оставаться в равновесии?
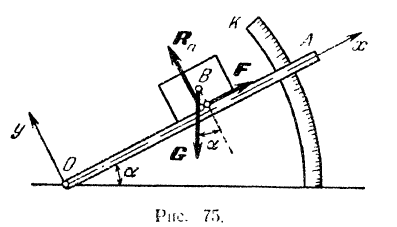
Решение:
Тело будет находиться на плоскости в равновесии под действием следующих сил: силы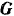 
тяжести тела, нормальной реакции 
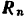плоскости и силы трения 
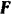. Проектируя эти силы на выбранные координатные ос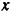и 
и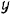 
, получим уравнения равновесия
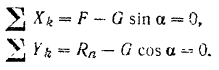
Из этой системы находим:
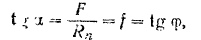
где 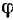— угол трения. Для равновесии тела необходимо, следовательно, соблюдение условия
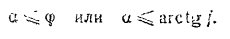
Найденная зависимость дает один из способов определения коэффициента трения скольжения в покое. Постепенно увеличивая угол наклона плоскости, замечаем (по шкале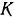 
) тот угол 
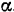, при котором тело начинает скользить по плоскости. Тангенс этого угла дает нам коэффициент трения скольжения для соответствующих материалов (тела и плоскости).
Аналогично решается задача об определении так называемого угла естественного откоса какого-либо грунта, т. е. наибольшего угла 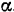наклона грунта к горизонту, при котором частицы грунта, находящиеся на откосе, остаются в равновесии:
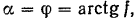
где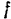 
— коэффициент трения между частицами грунта.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
