Угловая скорость тела как вектор. Выражение скорости точки тела в виде векторного произведения. Понятие о свободном движении твердого тела
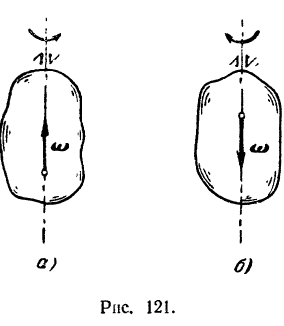
Вектором угловой скорости тела называется вектор, направленный вдоль оси вращения так, чтобы, смотря с конца его, мы видели вращение тела совершающимся против хода стрелки часов (рис. 121, а и б).
Вектор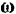 
есть вектор скользящий, т. е. за его начало можно взять любую точку, лежащую на оси вращения тела.
В случае вращения тела вокруг неподвижной оси модуль этого вектора равен абсолютному значению производной от угла поворота тела по времени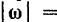 
.
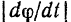Задание вектора 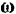угловой скорости полностью определяет вращательное движение тела, так как позволяет знать положение оси вращения тела, сторону вращения и численное значение угловой скорости.
Отложим на оси вращения из какой-либо произвольной ее точки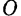 
вектор 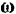угловой скорости тела и из этой же точки проведем радиус-вектор 
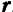, определяющий положение данной точки тела (рис. 122).
Вспоминая еще раз (стр. 62) понятие о векторном произведении двух векторов, мы придем к выводу, что скорость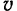 
любой точки вращающегося твердого тела равна векторному произведению вектора 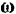угловой скорости тела на радиус-вектор 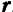данной точки 
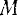(если за начало этого радиуса-вектора взята точка на оси вращения тела):
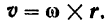
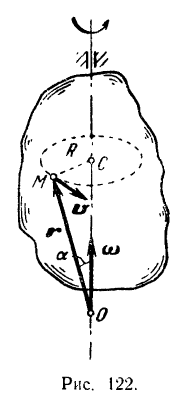
В самом деле, из прямоугольного треугольника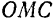 
будем иметь 
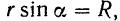, где 
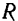— расстояние точки 
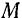до оси вращения. Модуль векторного произведения
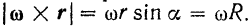
Направлен же вектор
так же как и вектор 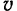, перпендикулярно к плоскости 
и в сторону вращения тела, т. е. в сторону, откуда кратчайший переход от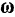 
к 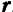будет представляться совершающимся против хода стрелки часов.
Любое движение свободного твердого тела, как это доказывается в более полных курсах механики, можно считать составленным из двух движений: поступательного движения со скоростью произвольно выбранной точки тела (полюса) и вращательного движения вокруг некоторой оси, проходящей через выбранный полюс.
Каждому моменту времени (мгновению) соответствует свое положение этой оси в пространстве и относительно данного тела, и поэтому, в отличие от неподвижной оси, она называется мгновенной осыо вращения тела.
Угловая скорость вращения тела вокруг мгновенной оси называется мгновенной угловой скоростью.
Мгновенную угловую скорость тела, как и в случае вращения тела вокруг неподвижной оси, можно представить в виде вектора, направленного вдоль мгновенной оси. Вследствие непрерывного изменения положения мгновенной оси, вектор 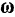мгновенной угловой скорости изменяется со временем не только по абсолютной величине, по и по направлению.
Скорости точек тела, лежащих на мгновенной оси, равны нулю. Отсюда следует, что скорости любых точек тела при его вращении вокруг мгновенной оси можно вычислять в каждый данный момент времени по установленной выше формуле (91)
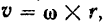
где 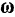— соответствующий данному моменту времени вектор мгновенной угловой скорости тела и — радиус-вектор точки, имеющий начало на мгновенной оси вращения.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
