Оглавление:









Удар по телу, вращающемуся вокруг неподвижной оси
- При столкновении с объектом, вращающимся вокруг неподвижной оси, на опоре возникает реактивный ударный импульс 5e. Точка на оси 2 подвижной системы координат, связанной с телом, вдоль оси вращения. Плоскость x2 рисуется через ось вращения и центроид c тела. Оси y, вместе с х-и 2-оси, формирует правильную систему координат оси рис. 170. Предположим, что ударный импульс 5 прикладывается к точке o, расположенной на оси x. Для этого достаточно найти точку o пересечения линии действия импульсного импульса 5 и плоскости xg.
Нарисуйте ось x через точку Сделайте o перпендикулярным оси вращения r и переместите ударную линию 5 вдоль ее линии действия в точку d. in сложение, 01 — i, ОА а, ов b, — — з д, — угол первой скорости тела Удар, o — угол Скорость тела в шоке. Определить проекцию оси смещения декартовых координат, связанных с объектом, вращающимся вокруг реактивного ударного импульса 5l, a in wu и неподвижной оси 2 Решите систему уравнений. ЛК ВХ Т б — 1 3aua е — Д — Ахх bxb по— 1л Эта система уравнений является результатом применения теоремы Об изменении главного вектора импульса и изменении главного момента импульса, приложенного к мгновенной силе проекции декартовых координат на движущуюся ось.
В классической механике изучаются движения материальных тел, происходящие со скоростями, малыми по сравнению со скоростью света. Людмила Фирмаль
Проекция ударного импульса струи на ось вращения и 8j входит только в 3-е уравнение системы. Таким образом, можно вычислить только сумму, причем каждую из этих величин Не определяется индивидуально. Если верхняя опора b создана в виде подшипника, то она вычисляется из 3-го уравнения системы При столкновении с объектом, вращающимся вокруг неподвижной оси, реактивный импульс удара исчезает это очень важно при построении Если он работает правильно, то должны быть выполнены следующие условия 1 ударный импульс 5 поворот к вертикали xy плоскость через ось вращения и центроид тела, т. е.
Ось вращения тела 2 должна быть главной осью инерции на пересечении с вертикальной плоскостью xy, включая импульс 3, т. е. L 0. 3 точка приложения b ударного импульса 3 должна находиться на расстоянии от оси вращения g на расстоянии укороченной длины физического маятника. Ось усиления совпадает с осью вращения. Данное тело, т. е. При отсутствии реактивного ударного импульса точка приложения b a и ударного импульса 3 называется центром удара.
Решение задачи определения местоположения центра удара сводится к выполнению трех условий, описанных выше. Учитывая скорость объектов, сталкивающихся в начале столкновения, силу тяжести, момент инерции этих объектов и положение их центра тяжести, необходимо выполнять задачи, определяющие реактивность. В случае ударного импульса рекомендуется решать его в следующем порядке 1 указать движущиеся координатные оси, связанные с телом выбрать ось 2 вдоль оси вращения и нарисовать плоскость x2 Ось вращения и центр тяжести тела c, ось x должны проходить через точку o пересечения линии действия импульса и плоскости xg.
Выберите ось y, а также ось x и ось z Сформирована правильная система координат оси. 2 Исследуйте каждое тело столкновения индивидуально, нарисуйте импульс внешней мгновенной силы и примените теорему об изменении основного момента импульса в приложении Приложите мгновенную силу к движению тела, вращающегося вокруг неподвижной оси. Для любого поступательного движения сталкивающегося объекта примените теорему изменения к этому объекту Основной вектор импульса приложен к мгновенной силе. 3 После определения системы уравнений, обобщенных в предыдущем пункте, определите величину ударного импульса 5 в конце ударного импульса.
Создайте систему уравнений 1, которая применяется к объектам, вращающимся вокруг фиксированной оси. 5 после решения системы уравнений 1 Определите проекцию искомого реактивного импульса импульса. Если в условиях задачи задано условие удара 5 и угловая скорость объекта в конце удара, то 2-я и 3-я точки решения задачи опущены. Задача 441. Удар наносится по корпусу, он вращается вокруг неподвижной оси и создает реактивный ударный импульс на опоре. Как известно, при вращении несбалансированного тела в опоре возникают дополнительные силы реакции. Можно ли найти условие, при котором ударный импульс в опоре и дополнительная сила реакции в опоре будут равны i Ноль solution.
Для того чтобы дополнительные опорные реакции исчезли, ось вращения твердого тела должна быть главной центральной осью тела. Inertia. In в этом случае центроид c является Ось вращения, то есть эксцентриситет равен нулю ПК о. 1 Для того чтобы ударный импульс в опоре был равен нулю, необходимо выполнить 3 условия, описанные в обзоре теории. Согласно 3-му условию, пункт Импа Ульс удара Он называется центром удара и должен быть защищен от оси вращения Стояние, равное укорочению длины физического маятника, оси Вес совмещается с осью вращения тела, то есть, xc-расстояние от центра тяжести объекта до оси вращения, эксцентриситет pc. So.
- Иначе говоря 2 если pc 0, вы получаете b oo, поэтому легко увидеть, что условие 1 и 2 несовместимы. То есть, точка приложения ударного импульса должна быть бесконечно удалена от оси вращения .Это почти невозможно .Поэтому невозможно одновременно снять реактивный ударный импульс и дополнительную реактивную силу опоры .Задача 442 .Пуля Р-веса падает к центру тяжести на неподвижную круговую цель веса и радиуса r на скорости f Перпендикулярно плоскости мишени .Мишень находится в своей плоскости и может вращаться вокруг постоянной вертикальной оси на расстоянии от центра тяжести мишени .Равна половине радиуса .Определить величину реактивного ударного импульса упорных подшипников а и в, предполагая, что удар является неинерционным .ДС ВС к .Возьмите цель в виде однородного круглого диска .Ресепия .Выберите ось перемещения, связанную с целью вращения .Ось 2 совмещена с осью вращения .плоскость xy рисуется через ось вращения 2 и центроид c мишени .
На ней изображен ударный импульс внешней силы 5-ударный импульс, приложенный к центру тяжести мишени, 5La, 5Bg-составляющая реактивного ударного импульса .Величина ударного импульса 5 и угловая скорость мишени в конце неупругого удара неизвестны, поэтому рассмотрим и определим движение пули и мишени индивидуально .Ударный импульс V подается на пул со стороны мишени .Примените его к движению пули, теореме об изменении импульса и применению к мгновенной силе .0 Здесь заданная скорость пули в начале удара равна неизвестной скорости пули в конце удара .Описывается теорема об изменении главного момента импульса, приложенного к мгновенной силе относительно оси 2 для цели motion .At в начале удара цель была неподвижной .То есть, o 2 0 .момент инерции мишени относительно оси Z Так ..
Ось X Центр тяжести c непосредственно через Импульс удара прикладывается Штосселем 5 .выберите ось Y, чтобы сформировать правильную систему координат с осями X и Z . Людмила Фирмаль
Рассматриваемый. Что мы решили И затем Что 0 0 РА 3 Одновременные уравнения i и 2 Определение 3 2 3 О2 так П ПРОМАЛЬП не 2Р, р, р п 2 Для определения величины составляющих реактивного ударного импульса запишите целевую систему уравнений 1. LХ ЛГ—Л д В Н ХС 0 у ЛГ н я Д Л- — — О Д — 8aha ХВ 8 1-1ug о, 2-В12. 4 im- Ударный импульс 5 параллелен основному y. Следовательно, 5l. 0, 5u 5, 5, 0. Координаты центроида с Равный Мишень лежа Ось 5 икс США b- 6 honora b-это подшипник. 5-й. 0. Иначе говоря ось y перпендикулярна плоскости симметрии материала target. So. .hg 7 8 ось X является симметричной оси мишени .Так .. ХС 0. 9 Угловая скорость цели в начале удара равна нулю — 0.
Формула 3 4 5 6 7 8 9 и используем 10 и формируем уравнение i, учитывая, что a b 1r Второй После решения кондукторной системы уравнений найдите искомые значения составляющих упорного подшипника а и реактивного ударного импульса подшипника В. О 2аЧР 4-2р 2 О Г р 2pyy В точке мишени, где, как считается, был применен ударный импульс 5 Задача 443. In задача не должна быть отправлена в поддержку Мы решили эту проблему it.
Для того чтобы ударный импульс 5 не передавался на опору, необходимо выполнить следующие 3 условия Это условие выполняется. 2 ось вращения r должна быть главной осью пересечения с вертикальной плоскостью, где импульс импульса 5 равен xx,. , 3 точка приложения ударного импульса 5, называемая центром удара, должна быть отделена от оси вращения 2 на расстояние физическое уменьшение длины маятника, равное оси усиления. Он соответствует оси вращения тела Р ы г 2 и r, поэтому 1 r. Г к s 2 Поэтому ударный импульс 5 следует прикладывать к точке на расстоянии от оси вращения 2 до r. Предварительный заказ Вертикаль и центр тяжести Инерция в определенной точке.
Этот результат можно получить непосредственно из решения предыдущей задачи. Фактически, если расстояние от точки приложения ударного импульса 5 до оси вращения r находится в месте y, то формулы для и предыдущих задач 3 и 4 принимают следующий вид И затем e p g sh П, Г 0 2 2 px p p r- 1 2 Значения этих 5 и ed1 должны быть присвоены правой части 2-го уравнения i system. In кроме того, правая часть уравнения ii всех систем Реактивно-ударные импульсы будут равны, потому что они исчезнут Ноль о 2, — ш1г — 0. 3 Формула 3 — 5 и со. Присвоим значение 2 из формул i и 2 и найдем i xc y m и w1 0 Значение, определенное выше i g. Задача 444.
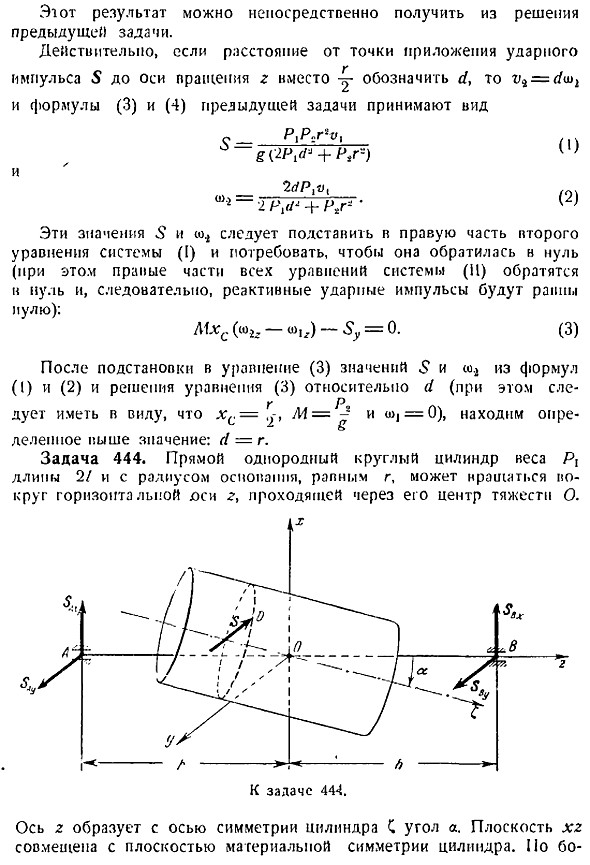
Прямой, равномерный, круглый цилиндр с радиусом основания равным весу p, длиной 2, r может вращаться вокруг горизонтальной оси psi r, проходящей через центр тяжести o. Ось 2 образует ось симметрии и угол a цилиндра c. Плоскость x1 совмещена с плоскостью симметрии материала цилиндра. На стороне цилиндра который отдыхал Удар наносится, и ударный импульс 5 — точка приложения ударного импульса 5 О находится на стороне цилиндра плоскости xy, x0 0, 5 г. Подшипник a и b ударные импульсы, учитывая, что удар является неупругим. АО-ОВ-К. Подвижные координатные оси обруча соединены с цилиндром. Решение.
Нарисуем импульс внешней мгновенной силы 5-ударный импульс, который прикладывается к боковой поверхности цилиндра lg pu-составляющая реактивного ударного импульса Подшипники a и b Угловая скорость o. Поскольку цилиндр ударной копии не задан, примените теорему к движению цилиндра, чтобы определить его. Приложение к вращающемуся валу мгновенной силы g В. 5 1. 1 Л-И В этом деле н 4 0. L 1 Таким образом, выражение 1 принимает вид РГ 5г 2. Откуда 2 Сконфигурируйте систему ускорения 1 в цилиндрах для определения величины составляющих реактивного ударного импульса. 5lx 5 1х — 5х Лу Цу −0, 1 г — г Ауа — 11 Б — б- — Ага —. — О В зависимости от условия 5 −5. So.
Смотрите также:
Предмет теоретическая механика

