Оглавление:









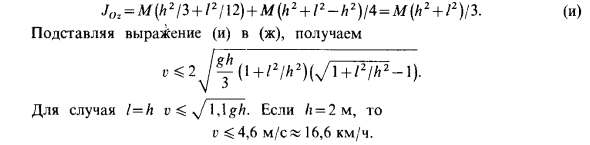

Удар двух тел
- В примененной задаче вы обычно сталкиваетесь с ударами, когда два объекта движутся постепенно или вращаются вокруг параллельных или совпадающих осей. Рассмотрим некоторые особенности общей теоремы и применение теоремы Карно в этих случаях. Два тела 1 и 2 с массой и t2 продвигаются сразу после удара (рис. 157). Скорость до нажатия g, d2. После удара Привет, соответственно d2. Ударное тело не имеет ударного трения. Ударный импульс в этом случае направлен вдоль всего Нормальный в точке контакта, то есть нормальный вдоль так называемой линии удара.
В случае центрального удара линия удара проходит через центр тяжести тела. Мы применяем теорему к изменению импульса, поскольку он сталкивается с каждым телом в отдельности. Существует m ^ m ^ S; t2y2 t2 2 = 5g (19) Согласно закону действия и равенства реакции, когда два объекта попадают в St = S2, мы можем поэтому получить из (19). mlul + m202 = mlvl + m2v2, (20) Другими словами, импульс, когда два объекта сталкиваются, не изменяется. Если удар полностью неэластичен, скорость объекта после удара равна и равна и. С (20) рН, + м2 При прямом столкновении двух объектов скорости до столкновения vt и t> 2 направлены вдоль линии столкновения, проецируются из (21) на линию столкновения и т. Д.
Точка, на которую не действует никакая заданная сила, движется на плоскости, вращающейся с постоянной угловой скоростью ш вокруг неподвижной оси, с которой она неизменно связана. Людмила Фирмаль
Где v15 v2 алгебраическое значение скорости. Для того чтобы удар произошел, скорости объектов vt и v2 должны быть направлены в одном направлении, а их значения должны удовлетворять условию v> p2. Прямое столкновение центра двух тел с каждым телом в первой и второй фазах применяет теорему к изменению импульса проекции на ось Ox, направленную вдоль линии столкновения (рис. 158). получить Здесь и приведены общие скорости тела в конце первого этапа. 5) S i и S1, S i ударные импульсы первой и второй фаз удара соответственно. К формуле (22) необходимо добавить формулу коэффициента восстановления по ударному импульсу. У нас есть k = S ilS = S ilS 2. (22 ).
Получено семь алгебраических уравнений (22) и (22 ). Из этих уравнений и i> 2 и коэффициент восстановления k. В частности, из уравнений (22) и (22 ) можно получить = (23) ( . J; 1 1 + (24> J J (22) и (22 ) и их результаты могут быть использованы для расчета потерь кинетической энергии объекта To T при столкновении. <25> Абсолютное упругое воздействие двух объектов, A = 1 и 7 0 = T, то есть не происходит потери кинетической энергии. Для абсолютно неупругих ударов fc = 0 и 125 ) При использовании скоростей r, , v2 u, потерянных объектом во время столкновения, потеря кинетической энергии также может быть получена в форме теоремы Карно для столкновения двух объектов. (25 ).
При абсолютном неупругом столкновении двух прогрессивно движущихся тел каждого тела наложенная связь не фиксируется, и условия St H = 0 и 52nd = 0 не выполняются индивидуально. Они были использованы для вывода теоремы Карно для системы. Но условия двух тел соблюдены S u = Siu + S2u = (Si + S2) u = 0, (26) с того времени S = Si + S2 = 0, поэтому теорема Карно (25 ) остается в силе. Она может быть получена непосредственно путем преобразования энергии потерь gii, примените результаты (22) и (22 ) без использования условия (26). Условие влияния двух прогрессивно движущихся объектов (26) расширяет сферу действия теоремы Карно.
Из теоремы Карно (25 дюймов) для двух объектов прямое воздействие этих объектов на центр дает общую скорость объекта после удара. t + t2 Особый случай. 1. Пусть m (, m2 и vx, v2 масса и скорость первого и второго объектов соответственно до столкновения, где 1> 2 = 0. В этом случае кинетическая энергия объекта до столкновения равна T0 = m1vf 2. Общая скорость после прямого удара, абсолютно неэластичная T Кинетическая энергия тела после удара = ( 1 + 2) ^ = ^ ^ 1 = ^ (27) Потеря кинетической энергии, затрачиваемой на деформацию тела, Для m2 mx, установите m2 (m, + m2) i согласно (28) T0 TxT0, Другими словами, почти вся энергия, которую тело имело до удара, расходуется на деформацию тела.
Такие случаи возникают при ковке и других подобных случаях. В этом случае m2 это масса наковальни вместе с ковкой (еще до удара), а mx и v масса и скорость молотка до воздействия на ковку. Энергия тела при ковке расходуется на преодоление различных сопротивлений при последующих движениях, T = —T0kO, Другими словами, энергия не теряется, чтобы преодолеть сопротивление. Очевидно, что чем больше м2 по сравнению с тх, тем эффективнее молот. 2. В случае u1 u2, r2Tm2 + w2), предполагая потерю кинетической энергии самого столкновения Т = ~ Ч х К. Такие случаи возникают при забивании свай, костылей, гвоздей и т. Д.
Необходимо соблюдать условия, чтобы максимально повысить эффективность этих процессов. Гнездо или молот (молоток), r скорость до столкновения, м2 и i> 2 = 0 масса ворса или костыля (коготь) и скорость до столкновения соответственно. Масса для разумного использования энергии должна быть значительно меньше массы женщин и молотов. Вся такая кинетическая энергия женщины или большого молотка не расходуется на деформацию при ударе, а передается в кучу или костыль, который движется вместе с женщиной или большим молотком с помощью молотка или молотка. Эта энергия расходуется на преодоление сопротивления движению кучи или костыля.
- При рассмотрении влияния двух объектов, вращающихся вокруг одной оси или параллельных осей, к каждому объекту должна применяться теорема об изменении момента движения или теорема Карно. Применяя теорему об изменении импульса одновременно к двум объектам, когда объект вращается вокруг параллельной оси, неизвестный момент ударного импульса вводится в точке, которая фиксирует, по меньшей мере, одну ось вращения. Сами эти моменты неизвестны. В следующем разделе мы рассмотрим применение общей теоремы при воздействии на один объект, вращающийся вокруг неподвижной оси.
Здесь мы сосредоточимся только на некоторых особенностях применения теоремы Карно к системе двух вращающихся тел. Когда два объекта вращаются вокруг одной оси (рис. 159) <9XO2 это угловая скорость ω до столкновения, то же направление вокруг этой оси и J2 и момент инерции co2 Если удар полностью неэластичен, можно применить теорему Карно. Здесь выполняется условие применимости этой теоремы для двух объектов. Так как S = Sj + S2 = 0, 5 й = 0. Где а> общая угловая скорость объекта после удара. coj o и , + UD < > 2 L + 4 (30) Такое же значение ω можно получить, применив теорему к изменению момента движения двух объектов вокруг оси вращения. Это сумма моментов ударного импульса от воздействия в этом случае 7 77D и Рис. 160 От подшипников.
Сообщим жидкости единственно возможное для нее перемещение, допускаемое связями, перемещение, при котором вся колонка совершает скольжение как целое на бесконечно малую величину. Людмила Фирмаль
Когда выступ на оси вращения равен нулю Не существует ударного трения между подшипником и выступом. Если объект вращается в противоположном направлении до столкновения, необходимо принять во внимание алгебраическое значение угловой скорости объекта (30). Пример 1. Груз массой t Перед падением на плиту 2 массой t2 он упал с высоты А без начальной скорости (рис. 160). Пластина 2, прикрепленная к пружине с коэффициентом жесткости c, вибрирует и имеет скорость вверх b2 => j2gh в момент удара. В этом случае пружина деформируется на значение X0 = . Определите максимальную величину деформации пружины с учетом того, что воздействие на тело совершенно неэластично.
Решения. Нагрузка перед ударом из за падения с высоты А имеет скорость v = y 2gh и является нисходящей. В результате абсолютно неупругого удара оба тела набирают одинаковую скорость r и продолжают двигаться вместе как одно тело. Применить теорему Карно к мгновенной суперпозиции ограничений, чтобы определить эту скорость (А) Условия применения этой теоремы выполнены. Другими словами, 5 + S2 = 0 и сила удара от пружины равна нулю, поэтому 51st + 52y = (5, +52) d = 0. В этом случае кинетическая энергия до столкновения T 0> = mlv1, l2 + m2vI2l2. T = (m1 + m2) n 2. Скорость кузова Каждый равен (t> t и) Подстановка значения количества, полученного в (а) после простого преобразования, приводит к следующему. Весной не произошло скорости и может, импульс меняется вниз.
У нас есть (В) Изменение скорости груза из за Улара Примените теорему об и слэб к эффекту проекции на ось Ох, (С) E количество поездок до и после забастовки = T, , + t, ( 2 ; e, = b + .) Внешние ударные импульсы, которые влияют на ударное воздействие, могут создаваться только пружинами. Импульс безударной силы во время удара следует игнорировать. Пружина генерирует силу упругости, и в результате она получает удар из за деформации, и есть время для генерации нс между ударами. Так что S = 0 и получите снова из (с) Существует скорость, и движущееся тело деформирует пружину. Максимальная деформация возникает при скорости объекта e = 0. Согласно теореме об изменении кинетической энергии от момента после столкновения до остановки тела при изменении направления движения r m0 = л (G).
При максимальном напряжении Inpiosugi Он движется A. = Lo + 5, Lo = Заменить расчет Ск + пг) Решение квадратного уравнения, отбрасывание знака минус перед квадратным корнем и отрицательное значение z дает Работа внешняя по формуле Аббревиатура Максимальная деформация пружины e = c, получаем X = Xn + 7 ^ 2 + 2X <Приобретено по примеру Пример 2. 1 высота прямоугольный контейнер Находится на платформе, которая движется по прямой траектории на высокой скорости (Рисунок 161) Определяет требование скорости платформы, при котором NS наклоняет контейнер вокруг неподвижного конца, когда платформа мгновенно останавливается. Фиксация ребра контейнера не препятствует вращению вокруг этого ребра.
Решения. Когда платформа остановлена, теорема применяется к изменению момента движения для неподвижного ребра Oz во время столкновения. (А) Это связано с тем, что импульс внешнего воздействия является только ударным импульсом, поэтому конец контейнера зафиксирован. Когда нет ударного трения, потому что оно пересекает ось Oz Как только платформа останавливается, контейнер начинает вращаться вокруг оси Oz с угловой скоростью ω. На момент перемещения контейнера относительно неподвижного ребра, KO1 = JO1 <0, (В) Рисунок 161 (А) Стоп позиции кинетической энергии Есть форма Угловая скорость <теорема Для угловой скорости контейнера Применимо к динамически меняющимся контейнерам Мы берем платформу в конце первой позиции … удар.
Представлено как Наконец, установите позиционер в наивысшую позицию Центр тяжести, то есть положение после вращения контейнера на 451. Чтобы предотвратить опрокидывание контейнера, угловая скорость в этом положении должна быть равна нулю, т. Е. T = 0. Внешняя сила контейнера это его сила тяжести P = Mg и сила реакции .V ребра Og. Таким образом, работа с внешней силой сводится только к гравитационной работе, когда центр тяжести поднимается на высоту (OS L 2). Реакция N равна нулю. У нас есть Y.AV = P (OC h 2), Где ОС у л2 + х2 2. Подставляя все величины, рассчитанные в (е), = Mg (J2 + H2 H).
Отсюда получаем следующие условия для скорости платформы, при которой контейнер не падает: анальный с памятью Через центр Инерционная две параллельные М (0С) 2. унция, Джо. , = Jc, + M (0 C) 2. Исключая JC из этих двух уравнений, JOj йо = M (OC) 2 (O C) 2 ; Jo = Jo. , + M (OC) 2 (OC) 2 . (Н) Момент инерции Джо. , Определяется по уравнению (13) (см. 4 Ч.3) для однородных прямоугольных пластин. Эта формула действительна, когда рассматривается, и вам нужно только заменить Lie . Существует JO: = M (h2 3 + l2 n) , (OS) 2 = (Л2 + 2) 4; (O C) = L2 4. После этого Джо = M (h2 3 + l2l 2) + M (h2 + l2 h2) 4 = M (h2 + l2) l3. Подстановка уравнения (u) в (g) дает v <2j ^ i + l1lh2) (^ + l2lh1 i). l = h o << l , для G i для него = 2 м, v <4,6 м с 16,6 км ч (А).
Смотрите также:
Задачи по теоретической механике
| Экспериментальное определение коэффициента восстановления | Центр удара |
| Теорема Карно | Задача Ньют |

