Оглавление:


Удар движущегося вагона о тупиковое ограждение
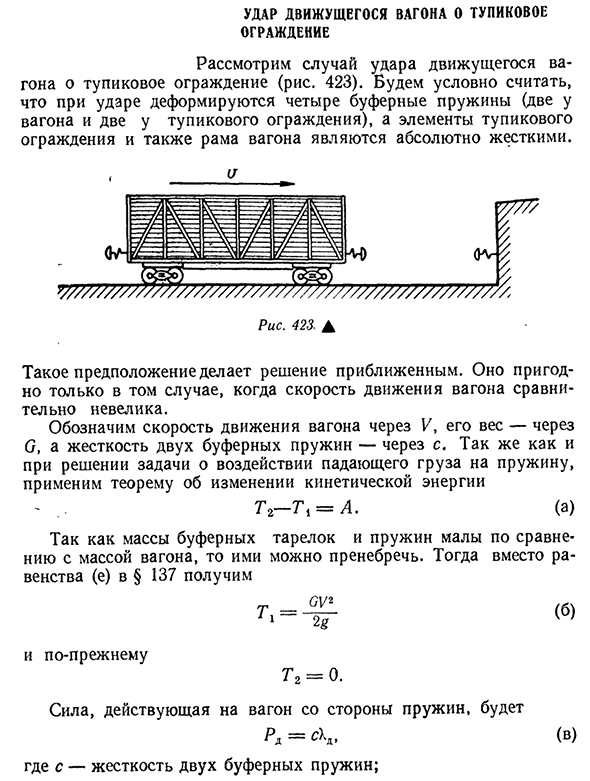
- Влияние автомобилей, движущихся в тупики Забор Рассмотрим случай, когда движущийся автомобиль врезается в тупиковое
ограждение (рис. 423). В случае столкновения буферные пружины (сторона транспортного средства и сторона тупикового ограждения) деформируются, а элементы тупикового ограждения и боковая
рама транспортного средства становятся полностью жесткими. И ЛЮКС Людмила Фирмаль
X.’XX’ икс \ \ \ — — —1 я не уверен……….. / ——- П. Один./ — Ю. Г. / / Г / / — Г / / » ‘-X Т~1п/ » Т Г / — — — — — ХV— 7Г — » ~ГХГ“ — 7г—— —— у Р Рис 423А Это предположение приближает решение. Он подходит только в том
случае, если скорость автомобиля относительно невелика. Покажем скорость автомобиля через V, а его вес-через 6, а жесткость двух
- буферных пружин-через C, а также решим задачу о влиянии падающей нагрузки на пружину, и тогда вместо§137 получим равенство (e). Ой (бел) И все же Т2=0. Сила, действующая на автомобиль со стороны пружины=SHD, (b) где C-жесткость двух буферных пружин; 509-величина суммарного сжатия двух буферов пружины (буфера
автомобиля и буфера защиты от тупика). Учитывая, что сила, действующая на автомобиль, выполняет отрицательную работу, мы получаем, p a Л2 2С * Если мы подставим выражения (b) и (C) в выражение (a)、 с хорошо у вас — _ ~ 2С Где вы определяет
е силу, возникающую после удара, P* — Y/ — y-. (16.6)P R и m e R. 60-тонная Людмила Фирмаль
груженая машина врезается в тупиковое ограждение, как показано на рисунке, двигаясь со скоростью 0,1 м/ с. четыреста двадцать три Таким образом, сжатие двух буферных пружин от силы P=1T равно X = 1 см, с=1Т/см=100т/м. По формуле (16.6) находим 2.5 т.
Смотрите также:
| Учет сил инерции при расчете троса | Понятие о волновой теории удара |
| Расчеты на удар | Собственные колебания системы с одной степенью свободы |

