Учет сил инерции при расчете троса
Пусть тело весом G подымается на тросе с ускорением а (рис. 139) Вес троса q. Если тело не опускается и не подымается, то сила N равна

Если тело ускоренно подымается с ускорением а, то для определения натяжения троса необходимо составить уравнение движения тела, взять вторую производную и получить ускорение. Однако, этого можно не делать, если использовать принцип Даламбера.
Принцип Даламбера — движущуюся систему можно рассматривать как находящуюся в равновесии, если ко всем ее точкам присоединить дополнительно силы инерции.
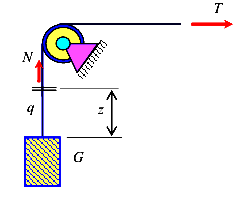
Силы инерции численно равны произведению массы на ускорение и направлены в сторону, противоположную ускорению

где g — ускорение свободного падения. Суммарная сила равна
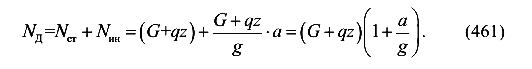
Окончательно имеем

В результате получаем формулу для динамического коэффициента

Используя динамический коэффициент и зная статическое напряжение, можно найти динамическое напряжение
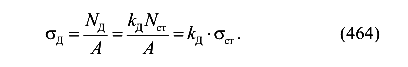
Окончательно имеем

Аналогично можно найти прогибы от динамической нагрузки

Если тело ускоренно опускается, то следует принимать а < 0.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Практический расчет сжатых стержней |
| Динамический расчет строительных конструкций |
| Расчет на удар |
| Прочность при переменных напряжениях |

