Задача №50.
Тяжелое колечко массы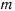 
надето на гладкую вертикально расположенную проволочную окружность радиуса 
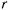. Колечко может свободно передвигаться по ней. В начальный момент оно находится в самой нижней точке окружности и ему сообщена начальная скорость 
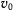. Найти условия, при которых колечко совершит полный оборот по окружности и определить давление на нее колечка, когда оно находится в самой верхней ее точке.
Решение:
На точку действует только одна активная сила — сила тяжести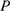 
, которая является консервативной силой и обладает силовой функцией. Поэтому для определения движения точки можно применить теорему живых сил. Эта теорема сразу дает первый интеграл — интеграл живых сил. Задавая положение точки углом 
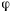, который ее радиус составляет с опущенной вниз вертикалью, интеграл живых сил запишем в виде
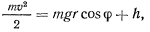
где 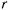— радиус окружности, 
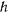— произвольная постоянная, определяемая из начальных условий. Подставляя сюда начальные значения 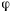и 
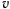, будем иметь
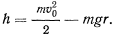
Тогда для скорости точки получим уравнение
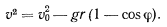
Чтобы колечко совершило полный оборот, скорость в верхней точке окружности должна быть отлична от нуля. Отсюда получаем условие для определения начальной скорости точки
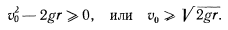
Давление колечка в верхней точке окружности определится из уравнения
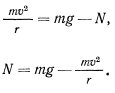
Таким образом, будем иметь после подстановки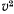 
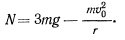
Здесь положительное значение реакция 
получает тогда, когда она направлена вверх.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
