Задача №54.
Тяжелая материальная точка вынуждена оставаться на совершенно гладкой плоскости, которая равномерно вращается вокруг горизонтальной оси, расположенной в самой плоскости. В начальный момент точка находится на оси вращения, а ее скорость направлена вдоль оси вращения и равна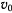 
. Определить закон движения точки.
Решение:
Выберем в качестве системы отсчета прямоугольную декартову систему координат, у которой ось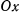 
совпадает с осью вращения, начало совпадает с начальным положением точки, а ось 
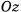направлена вертикально вверх. Уравнение вращающейся плоскости запишется в виде
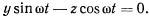
Для определения движения точки применим уравнения со множителями связи. Будем иметь
Пусть положение точки в плоскости определяется параметрами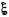 
и 
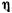, так что
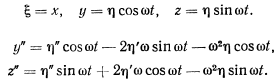
Исключая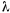 
из уравнений движения, будем иметь
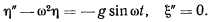
Общее решение этой системы имеет вид
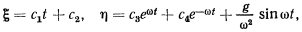
коэффициенты 
и 
определяются из начальных условий. После определения этих коэффициентов получим
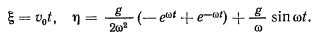
Для вычисления сил реакций связей рассмотрим одно из уравнений движения, например,
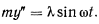
Подставляя сюда значение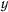 
, выраженное через 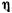, получим
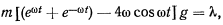
где 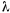и является нормальной реакцией связи.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
