Задача №53.
Тяжелая материальная точка движется по внутренней поверхности прямого кругового конуса, вершина которого обращена вниз, а ось симметрии вертикальна. Угол при вершине равен 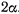 . В начальный момент расстояние точки от вершины конуса равно
. В начальный момент расстояние точки от вершины конуса равно 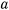 , начальная скорость равна
, начальная скорость равна 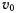 и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, которое она оказывает на поверхность конуса.
и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, которое она оказывает на поверхность конуса.
Решение:
Положение точки на поверхности конуса задается двумя координатами. Такими координатами могут быть расстояние точки от вершины конуса  и угол
и угол 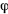 , который образует вертикальная плоскость
, который образует вертикальная плоскость  , проходящая через ось симметрии и точку
, проходящая через ось симметрии и точку 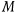 с неподвижной плоскостью
с неподвижной плоскостью 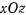 . Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости
. Рассматривая движение точки как сложное, состоящее из прямолинейного относительного движения в плоскости  и переносного вращения вместе с плоскостью
и переносного вращения вместе с плоскостью  вокруг оси
вокруг оси 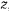 , для составляющих скорости будем иметь
, для составляющих скорости будем иметь
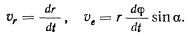
На рассматриваемую точку действует только сила тяжести и нормальная реакция поверхности. Поэтому будет существовать интеграл живых сил
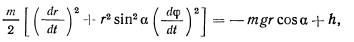
где 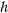 — постоянная живых сил.
— постоянная живых сил.
Действующие силы не создают момента относительно вертикальной оси 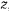 , а потому будет иметь место интеграл площадей, который легко преобразуется к виду
, а потому будет иметь место интеграл площадей, который легко преобразуется к виду
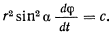
Здесь 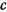 — постоянная площадей. Постоянные
— постоянная площадей. Постоянные 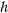 и
и 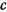 выражаются через начальные данные
выражаются через начальные данные
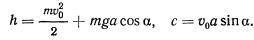
Полученные два первых интеграла позволяют определить траекторию точки на поверхности конуса. Для этого из полученных уравнений необходимо исключить время. Тогда будем иметь
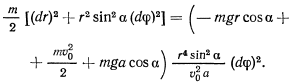
После разделения переменных будем иметь
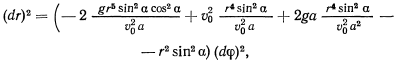
откуда, интегрируя, получим неявное уравнение траектории:
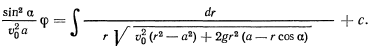
Для определения давления точки на поверхность конуса можно было бы воспользоваться естественными уравнениями движения, но такой путь оказывается сложным в данной задаче. Можно еще воспользоваться векторным уравнением движения
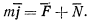
Давление точки на поверхность равно по величине и противоположно но направлению силе реакции 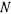 , которая зависит от действующих активных сил и от величины и направления ускорения точки. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. При определении ускорения точки можно заметить, что относительное ускорение направлено по образующей конуса, а в переносном движении точка движется по окружности, плоскость которой перпендикулярна к оси
, которая зависит от действующих активных сил и от величины и направления ускорения точки. Для определения давления требуется знать проекцию ускорения точки на нормаль к поверхности конуса. При определении ускорения точки можно заметить, что относительное ускорение направлено по образующей конуса, а в переносном движении точка движется по окружности, плоскость которой перпендикулярна к оси 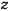 и имеет касательную и нормальную составляющие
и имеет касательную и нормальную составляющие 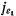 и
и 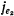 . Нормальная составляющая
. Нормальная составляющая 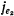 направлена ортогонально к оси симметрии конуса, а по величине равна
направлена ортогонально к оси симметрии конуса, а по величине равна
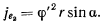
Добавочное ускорение коллинеарно с направлением ускорения 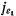 и численно равно
и численно равно 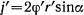 . На нормаль к поверхности дает отличную от нуля проекцию только составляющая ускорения
. На нормаль к поверхности дает отличную от нуля проекцию только составляющая ускорения 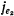 . Поэтому, проектируя уравнение движения на нормаль к поверхности конуса, будем иметь
. Поэтому, проектируя уравнение движения на нормаль к поверхности конуса, будем иметь
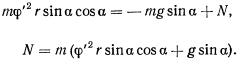
Подставляя значение  из интеграла площадей
из интеграла площадей
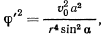
получим значение для
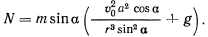
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

