Задача №17.
Твердое тело совершает сложное движение, которое сводится к трем мгновенным вращениям вокруг трех осей, расположенных по двум сторонам и одной диагонали квадрата (как указано на рис. 55), причем угловые скорости соответственно пропорциональны длинам сторон и диагонали квадрата. Привести эту систему мгновенных вращений к одному мгновенному вращению и найти результирующую угловую скорость вращения.
Решение:
Рассматриваемая задача сводится к приведению системы, состоящей из трех скользящих векторов, расположенных в одной -плоскости, к простейшему виду. Величина и направление вектора определяются по правилу сложения сходящихся скользящих векторов. Таким образом, величина результирующего вектора оказывается пропорциональной отрезку 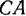 , а его линия действия параллельна отрезку
, а его линия действия параллельна отрезку 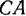 . Для полного определения линии действия остается указать точку, через которую она проходит. Заметим, что два вектора
. Для полного определения линии действия остается указать точку, через которую она проходит. Заметим, что два вектора 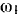 и
и 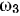 эквивалентны одному вектору
эквивалентны одному вектору 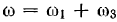 , линия действия которого параллельна линиям действия векторов
, линия действия которого параллельна линиям действия векторов 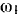 и
и 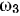 и делит пополам диагональ
и делит пополам диагональ 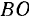 . Отсюда следует, что вектор
. Отсюда следует, что вектор 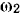 и вектор
и вектор 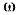 проходят через одну точку — середину диагонали
проходят через одну точку — середину диагонали 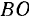 , а следовательно, и результирующий вектор ‘проходит через эту же точку.
, а следовательно, и результирующий вектор ‘проходит через эту же точку.
В тех случаях, когда у твердого тела закреплена только одна точка, мгновенное движение тела сводится к одному результирующему мгновенному вращению. При этом мгновенная ось вращения проходит через неподвижную точку. При определении «положения мгновенной оси вращения следует помнить, что скорости точек тела, расположенных на мгновенной оси вращения, равны нулю.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

