Оглавление:





Турбулентный поток, параллельный плоской пластине
- Уравнение массопереноса в турбулентном пограничном слое не может быть решено аналитически. Однако, подобно задачам теплопередачи и импульса, задача массопереноса «решается» применением интегрального метода кармана. 25, но это будет дано некоторыми. Подробно, так что предположение будет скорость турбулентного пограничного слоя является известным эмпирическим уравнением(13. 95). Поскольку эта формула была установлена для турбулентного движения в пограничном слое без массопереноса, ее использование в данном заключении может быть ограничено системами с низкой концентрацией диффузионных компонентов.
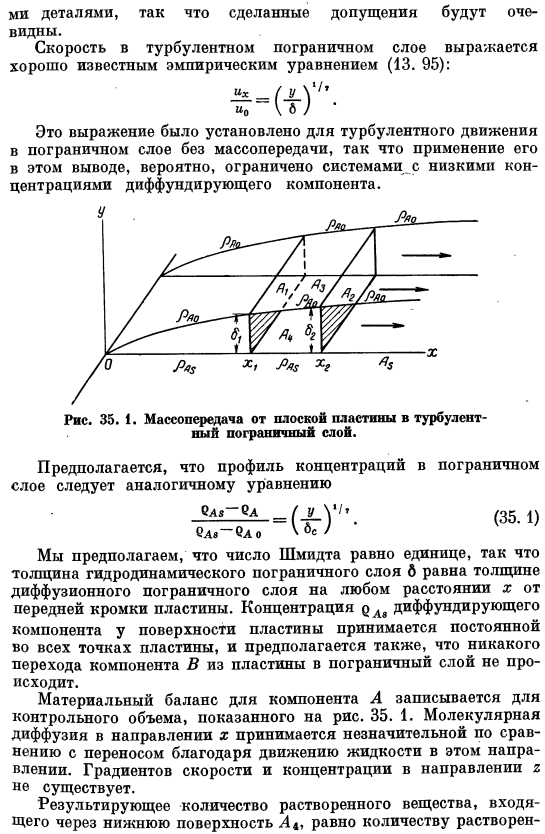
Предполагается, что профиль концентрации пограничного слоя следует аналогичному уравнению (35.1) Поскольку число Шмидта принимается равным 1, то толщина гидродинамического пограничного слоя b равна толщине диффузионного пограничного слоя на любом расстоянии x от передней кромки пластины. Предполагается, что концентрация диффузионных компонентов (>Dv) на поверхности пластины постоянна во всех точках пластины, а переход компонента B из пластины в пограничный слой не происходит. Материальный баланс компонента а записывается по отношению к контрольному объему, показанному на рисунке 5. 35. 1.
Если температура газа сильно отличается от внешней температуры, то стенки трубы имеют, более низкую температуру, чем газ, и тепло отводится по гильзе к стенкам трубы. Людмила Фирмаль
Предполагается, что молекулярная диффузия в направлении x пренебрежимо мала по сравнению с переносом за счет движения жидкости в этом направлении. Градиент скорости и концентрации в направлении 2 отсутствует. Количество, возникающее в результате поступления раствора со дна, равно количеству растворенного вещества Утечка материала из верхней части 4₃ и поверхности 4]и Л. In устойчивое состояние. Поток по формуле(3. 1) будет написано с помощью U / eliso8ay4 + / Ueli owl 74 + / / ешь » и soza 74 = = Л * о (0л.- 0л. Л — (35-2)) В поверхности 4, cosa = — ih, и в поверхности 4₃, cosa =and», и таким образом、 И * Aih aA + / 16₄₀ » cosa A 1A-D DAIH la = = Л Кэ (ешь » — e₄eat) Ил.
- Чтобы исключить вещество полового члена, вся поверхность . Запишите полный материал, включая поток растворенного A₃ Баланс громкости // oohOA-/ / она «74 +Л8 » Соза 74 = / / г (е—ХЛ>) АА- (35.4) Можно ограничить анализ разбавленными растворами с низкой концентрацией диффундирующих компонентов и предположить, что плотность жидкости одинакова по всей границе layer. So, можно также разделить каждый член формулы (35.4) на плотность e и умножить pDo. Это тоже константа. Результатом этих действий является уравнение (35. 5) показана и разрешена по отношению к потоку через поверхность. Затем мы подставляем формулу (35.5) в Формулу.
Все поверхности имеют одинаковую ширину в направлении Z. Поскольку ни одна из переменных не является функцией a, выражение (35. 6) может быть описана как простая интегральная сумма. /(ешь-СЛО) «х ^ — / (ОА-ешь)» хы! ’= ’/ ►.(1стл.- …[] (>- (35.7) Когда длина xa-xx приближается к нулю, левая часть уравнения (35.7) приближается к значению производной.
Так как тепло, переносимое от основания стержня, рассеивается в окружающую среду конвекцией, то задача может быть решена в результате сокращения уравнения (2-13) до членов, описывающих аксиальную теплопроводность и отдачу тепла конвенцией. Людмила Фирмаль
Правая сторона может быть применена к сегменту конечной ширины в направлении a, но она может быть применена к сегментам бесконечно малой ширины Lx в направлении x、 Здесь.* Термины под знаком интеграла, включая концентрацию, могут быть переписаны следующим образом: СЛО-О₌. баррель.- _₁_бл /i⁴⁴ ’ эль.- оло Элс-Эло Местная скорость-это (35.10) (35.11) Формула(35. 10) и (35.И Формула(35. 9) присваивается и интегрируется 25.Результат、 (35.12) Уравнение(13. 102) в точке 13 толщина пограничного слоя равна 6 = 0,376 *(не*) •• Если продифференцировать это уравнение、 (35.13) (35.14) Значение уравнения(35.14) неизвестно 0-ва Считайте фракцию k ^в разбавленном растворе.
Если в свободном потоке отсутствует диффузная составляющая, то это значение равно 1.Если объем, переносимый с пластины, незначителен, то формула (35. 14).Об этой части Как было согласовано в case. In цифра 0 0, полученное значение для K, L? Получите решение, аналогичное решению для передачи тепла Sec. 25.Умножьте обе части уравнения на 1Ц°Eи -.И затем… Я * Chilv (35.15)) Первоначально число Шмидта было принято равным 1, поэтому диффузионный слой и гидродинамический пограничный слой можно было считать одинаковой толщины.
Смотрите также:

