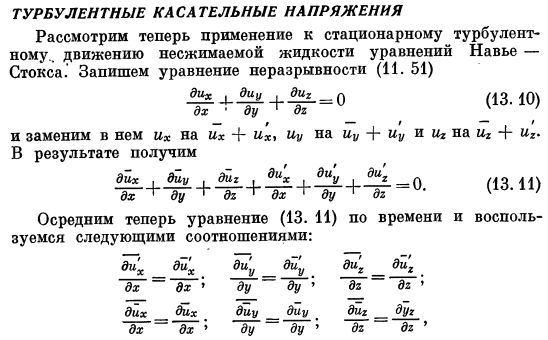




- Далее рассмотрим приложение к установившейся турбулентности. Уравнение Навье-Стокса движения несжимаемой жидкости. Уравнение неразрывности (11. Пятьдесят одни). Ди * я Диу к копать —— =0 (13.10) ДХ * ду * ДГ » И заменить их 4-ю заменить Горо с Горо + Горо, и как результат Диу, Диг, Диг, ГУР, копать _l, за ЛФ 4Р Где формула(13.Следующая зависимость используется для усреднения по времени. Диг Диг Диу Диу ди2____________ ди2 ду ДХ ДХ ДГ ы Дих _ _ Дих. Диу _ Диу.
Точно так же и (13.12) (13.13). Со средой (13.14) (13.15)) у ’Х = У У’ У ’ 2 = 0 В результате Диг■Диу, ди2 с DX-1 — ДГ ^ — ДГ-у.3 «+ дю + — в°- Уравнение неразрывности заполняется пульсирующей скоростью. Ось TT » M (11P52): направление WLARKNmotion control Е » и 2 \(пропуск массы)、 «Lh(13 -, 4) y, приблизительно»•». д(уй) а, д(МИУ)с д (ihig), Диг ДХ Т ду 1 Д-Г 1-77 = =д * ними D *им\ $ ДХ〜\ Н22 и dhg Т ду*’)’ Если выражение (13.10) заполнено, вы можете легко увидеть, что левая сторона этих 2 выражений равна.
Следующим этапом преобразования уравнения движения является уравнение^ ставим выражения D * » нечеткие переменные среды!»Мы находимся в конце «3 3aTvM«.Средний разведен, и в порядке первого члена°D BC6X lenov ЭМ * е ( «* + » * ) * д、—-— dx — — — — — — — — — dx——-■^-{+ их + 2 + их’). (13.16) Так как средняя скорость yx постоянна во времени и yx = 0、 е(2tsX) в ДХ-у ’ И для первого члена уравнения(13.15)、 __ ДХ ДХ 1 ДХ ’ (13.17) (13.18) Эти преобразования использовали правила, такие как= di ^ — ste-dx из предыдущих соображений _ __ Турбулентный штраф означает, что их2 = 0, но их8 не равно нулю. О втором триместре беременности д = л-(yhyu + ihiu + а, 4-ihiu)= Ду-ду-ду.
- Экскременты 〜 yx и yy равны нулю, но среднее время произведения u ^ yy не равно нулю. как будет объяснено позже, за исключением случая изотропной турбулентности, в какой-то момент между ними существует высокая степень корреляции. Для остальных членов, получить их, а также д(ихи 2)_ Д(ихи 2) и D (ихи). dg dg’DG 1 Дих Дих л. ДХ-ДХ ’ д-р. dh. (13. Двадцать) ’(13.21)) (13.22) И (13. Двадцать три) Д их***, Д *ними D * их _ и их. &ых д * ых ду * * ДГ * д * * с * * ДГ * Формула среднего времени (13. 15) (13. 18)-(13. 23) заменители、 Канава d (yhyu). д(yhy2) ДХ ’ду’• ___1 д-р; с дх Эта формула содержит 3 дополнительных условия.
Эти термины становятся невозможными, если вы просто замените переменную в выражении (13.15) на ее среднее значение. Смысл этих терминов заключается в том, что среднее значение массы X = 0 и= 0 в усредненном по времени уравнении (II) будет более ясным. Среднее время напряжения является результатом усреднения напряжения, вызванного действием нормальной вязкости. Общее среднее напряжение определяется как m ^ x, m {, x, и сумма соответствующих вязких и турбулентных напряжений. Thx = thx 4 ″ Thx>(13. Двадцать шесть) Тух = Тух 4-Тух! (13.27) м = = м + + м; х. (13.28)) Величины xTuh и m ^ x представляют вклад турбулентного напряжения. Где уравнение турбулентности I.
Формально описывает, заменяя каждую составляющую скорости ее средним значением, и заменяя каждую составляющую напряжения полным средним напряжением. Чтобы это уравнение было правильным, уравнение(13. 25)-(13. 28) и должны быть последовательными. Это дает следующее определение турбулентной составляющей напряжения: Ых = — ЕУ?; (13.30) тихо = — Е » Х; (13.31) м ^ = —РХ. (13.32) Эти напряжения также называются напряжением Рейнольдса или кажущимся напряжением. Формула (11. 46), (11.19) и (I. Из (21) определяется полное напряжение установившегося турбулентного движения несжимаемой жидкости. 4х =—Р + 2р Дич ДХ(13. Тридцать три) г » х,1 ДУ Диу \ ц) (13. Тридцать четыре) Диг, Диг ’ Р 13.
Тридцать пять T2X-H (dg’DX) — pmhig. К концу месяца, уравнение неразрывности несжимаемой жидкости(13. 12) потому что есть те, которые разрушаются членами уравнения(13. 33)-13.
Смотрите также:
| Средняя и пульсационная скорости | Интерпретация напряжений Рейнольдса |
| Степень турбулентности | Турбулентная вязкость и путь перемешивания |
