Оглавление:



Турбулентное течение. Основные сведения
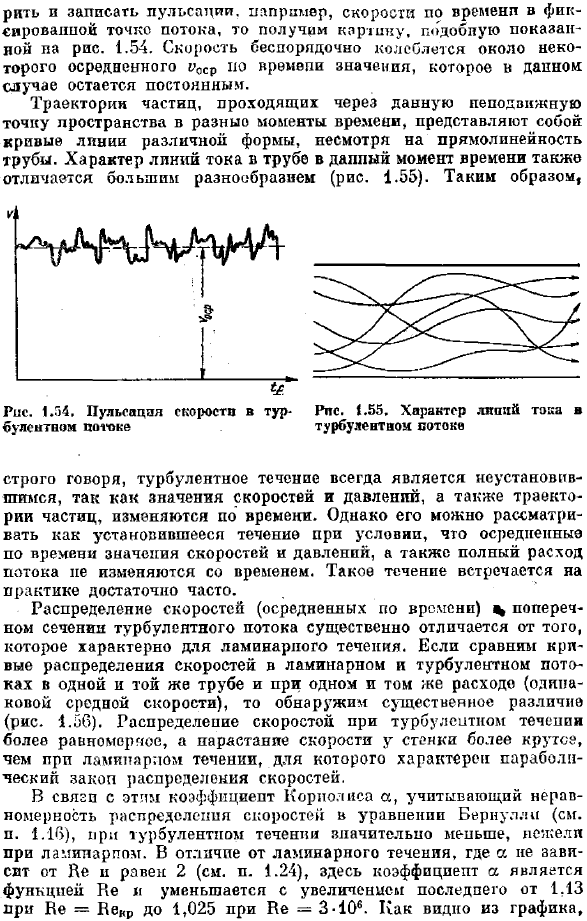
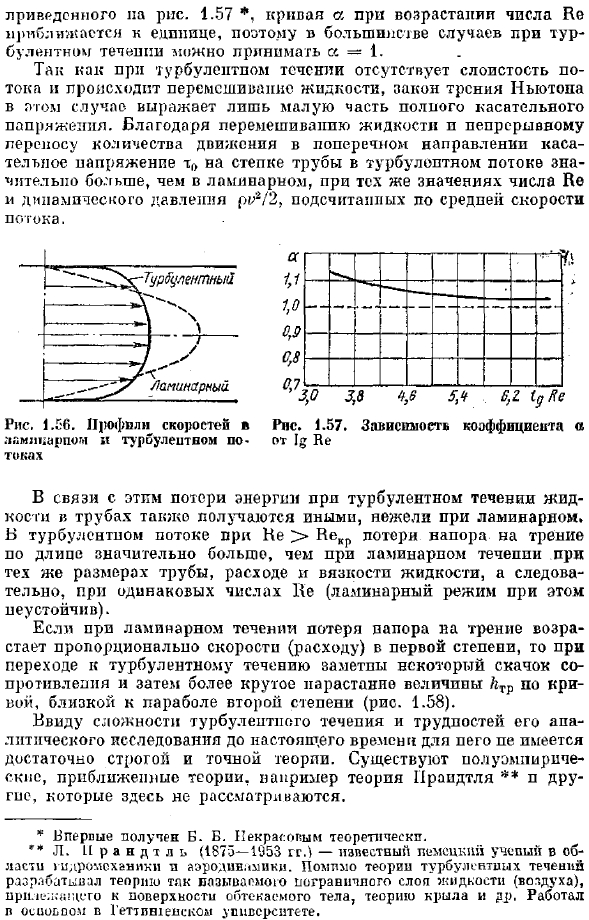
Турбулентное течение. Основные сведения. В разделе 1.22 было показано, что турбулентность характеризуется перемешиванием жидкости, пульсациями скорости и давления. Если вы используете особо чувствительный регистратор для измерения и записи пульсаций, например, временной скорости в фиксированной точке потока, вы получите изображение, как показано на рисунке 5. 1.54.Траектории частиц, проходящих через определенную неподвижную точку в пространстве в разных точках, являются кривыми разной формы, несмотря на прямолинейность трубы. Характер линий тока в трубах тоже очень разнообразны (рис. 1.55).Такой образ. И затем 。 4? Рис. 1.54.
Скорость беспорядочно колеблется вокруг определенных значений, которые были усреднены во времени, но в этом случае остается постоянной. Людмила Фирмаль
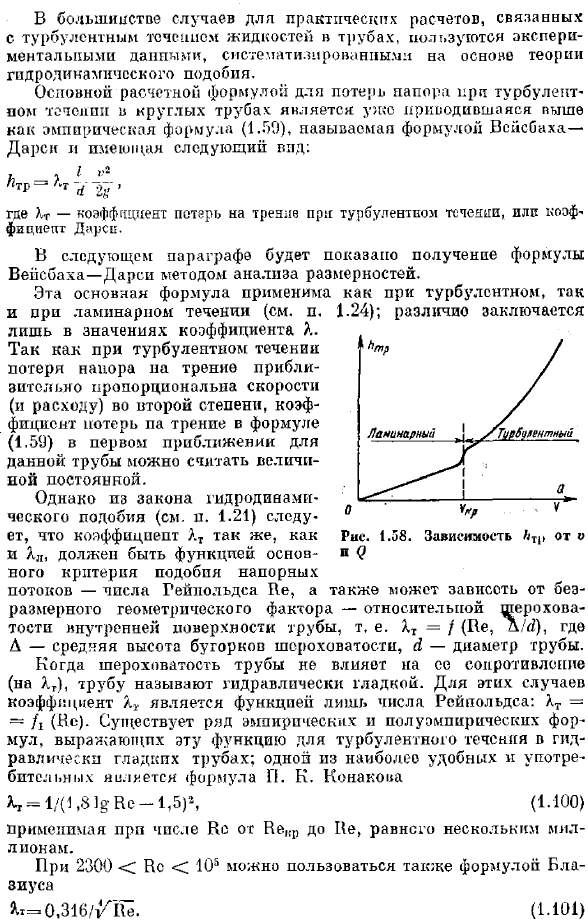
- Пульсации скорости в турбулентном. Строго говоря, турбулентность всегда нестабильна ■ 1В. pgamsya обусловлен величиной скорости и давления, а также траекторией движения частицы, изменяющейся со временем. Однако если средние по времени и суммарные скорости потока скорости и давления не изменяются со временем, то это можно рассматривать как устойчивый поток. Такой поток на самом деле очень распространен. Распределение скоростей (среднее по времени) поперечного сечения турбулентного потока^существенно отличается от характеристик ламинарного течения. Если сравнить кривую распределения скоростей ламинарного и турбулентного потоков при одинаковой скорости потока (одинаковой относительной скорости) в одной и той же трубе, то можно обнаружить существенные различия (рис.1.56).
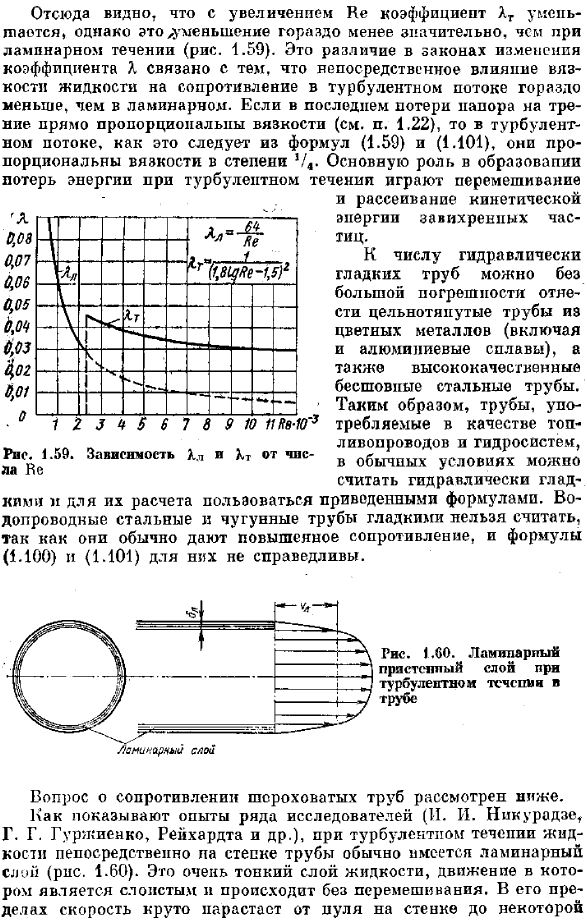
Распределение скорости в турбулентном потоке более равномерное, и увеличение скорости вблизи стенки более крутое, чем ламинарное течение, которое характеризуется параболическим отверстием в распределении скорости. В связи с этим коэффициент Кориолиса cc, учитывающий неравномерное распределение скорости уравнения Бернулли (см. раздел 1.16), в турбулентных потоках значительно меньше, чем в ламинарных. в отличие от ламинарного течения, где a равно 2 без зависимости от H. (N. см. 1.24), где коэффициент a является функцией He и уменьшается с увеличением последнего от 1.13 He до 1.025 he = Necr. 。Как видно из графика、 Как показано на рисунке 1.57*, кривая а с увеличением числа He не приближается к 1, поэтому в большинстве случаев можно использовать −1 для турбулентности.
- Как и в случае турбулентности, здесь не происходит расслоения потока и смешения жидкостей. Закон трения Ньютона в этом случае представляет собой лишь малую долю от общего касательного напряжения. Тангенциальное напряжение t турбулентного потока трубы, обусловленное непрерывным движением жидкости перемешивания и боковым импульсом, значительно больше ламинарного потока при том же динамическом числе давлений Ke м/м2, что и рассчитанное при средней скорости потока. * He> в турбулентном потоке на Kekr потери напора трения по длине значительно больше, чем у ламинарного потока того же размера трубы, расхода и вязкости. , А следовательно, и с одинаковым числом He (в этом случае ламинарный режим нестабилен).
В ламинарном потоке, если фрикционные потери напора возрастают пропорционально начальной степени скорости (течения), то при переходе к турбулентному потоку заметен определенный скачок сопротивления, причем МП на кривой вблизи 2-й параболы возрастает более резко (рис. 1.58).)、 Из-за сложности турбулентного течения и сложности его аналитического исследования до сих пор не существует достаточно строгой и точной теории для этого. Однако существуют только эмпирические и приближенные теории, например, теория гордости**, которую мы здесь рассматривать не будем. * B первый. Б. Некрасов приобретал теоретически. ** Л. Ирандтль (187-1953) известный немецкий ученый в области гидродинамики и аэродинамики, который, помимо теории турбулентности, разработал теорию так называемого пограничного слоя (воздуха), примыкающего.
В связи с этим можно видеть, что потери энергии турбулентного потока в трубе также отличаются от потерь энергии ламинарного потока. Людмила Фирмаль
- Винг и другие работали в Геттингенском университете. В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкости в трубе, экспериментальные данные систематизируются на основе теории гидродинамического подобия. Основная формула для потери давления турбулентного потока в круглой трубе называется формулой весбахса-Дарси и представляет собой эмпирическую формулу (1.59) в виде: Я к-7 -’ -’ тр-ЛТ» Где Xt-коэффициент потери тренда турбулентности, или коэффициент Дарена. В следующем разделе мы получим формулу Вейсбаха-Дульси с помощью размерного анализа. Эта основная формула может быть применена как к турбулентности, так и к ламинарному течению (см. раздел 1.24).
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:

