




- Вывод универсального распределения скоростей на основе маятниковой теории метода перемешивания. Теперь мы используем понятие траектории смешения для получения уравнения распределения скоростей в полностью развитом турбулентном потоке в круглой трубе. Затем с помощью этого уравнения получим уравнение потери давления при турбулентном движении. Далее мы покажем, как из этой зависимости выводится метод определения перепада давления при турбулентном движении.
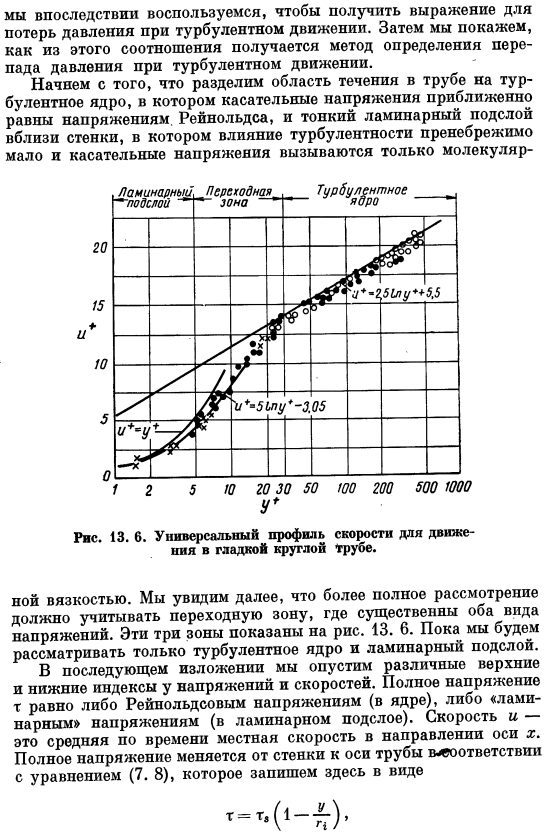
Во-первых, область течения в трубе разделена на влажный ламинарный подслой вблизи стенки, где тангенциальное напряжение приблизительно равно напряжению Рейнольдса, а турбулентный эффект незначителен, и тангенциальное напряжение вызвано только молекулой. Высокий viscosity. In кроме того, видно, что необходимо провести более полное исследование, учитывая переходные зоны, в которых важны оба вида напряжений. Эти 3 зоны показаны на рисунке. 13. 6.Здесь мы будем рассматривать только турбулентные ядра и ламинарные подслои. В следующей презентации вы опустите различные верхние и нижние индексы напряжения и скорости.
Полное напряжение m равно напряжению Рейнольдса (в ядре) или» слоистому » напряжению (в слоистом подслое).Скорость. Это средняя по времени локальная скорость в направлении оси X. Общее напряжение рассчитывается по формуле (7. 8) изменение от стены к оси трубы согласно theWhere m напряжение тока стены, и y расстояние от wall. In очень тонкий слоистый подслой, игнорируйте изменение в m、 1 и м = ч ^ = кон. (13.43) Если мы интегрируем это уравнение、 t8y = r-i или Тг( 13.44) В отличие от параболического распределения скоростей при ламинарном движении в трубе, скорость ламинарного подслоя зависит от расстояния от стены.
Это полезно, чтобы использовать отношения, чтобы познакомить их «*=/Т(13.45) Величина, называемая «фрикционная скорость» (динамическая скорость).Используя его, уравнение(13. 44) можно переписать на: И _ yi *и * V ’ (13.46) Безразмерное отношение скоростей слева от этого уравнения обозначается m+, а безразмерное расстояние справа-y *(последнее значение аналогично числу Рейнольдса). в свою очередь, распределение скоростей ламинарного подслоя можно выразить следующим образом: м + = м +. (13.47) Давайте сосредоточимся на турбулентном ядре. Игнорирование и запись вязких напряжений РД Т = ( € ) ’ — 1С-48> (Формула (13. 36) и 13.
В связи с тем, что производная всегда положительна, знак абсолютного значения опускается.) Чтобы идти вперед, сделайте 2 предположения. Оба эти предположения очень грубы. Их единственное реальное оправдание состоит в том, что они упрощают расчеты и конечная зависимость согласуется с экспериментальными данными. м = Тэ = Кобб、 1 = ку (13.49)где & — постоянная x.
- Второе редположение имеет смысл, потому что мы знаем, что путь смешения I должен быть сведен к нулю в стене, где турбулентность исчезает. Тогда формула(13. 48)в форме: (1350) И так оно и есть.、 И * = Ку ^. (13.51)) При интегрировании этого уравнения u * 1n y = Ki + C. Соотношение (13. Пятьдесят два) Константа c найдена при условии, что скорость u исчезает при малом значении y(например, y0). И у * в Ыб = з (13.53) 13.
Для поиска универсального профиля скорости, то есть профиля, который выражается формулой (то есть для всех u *и y0) любой ценой.、 И+ = /(L * (13.55) Уравнение для удовлетворения этих условий(13. 54) должны быть исправлены. Формула (13. 54) вводит переменную y +, переписывая ее в следующий формат: М + = 4(1Н ^ ._ 1Н ^)(13.56) Или И+ = —1pu + + cx. (13.57)) Формула (13. 57) должны выражать и как универсальную функцию y+.Поэтому имеет смысл предположить, что величина, которую можно описать как универсальную константу, то есть значение y +при u + = 0.Формулы, где K и c1-универсальные константы 13.
На рис. 6 показано большое количество данных dap о распределении скорости в диапазоне чисел Рейнольдса. Около 4000 1. оба предположения сводятся к тому, что движение вблизи стены аналогично движению вблизи границы полупространства. (Примечание, трансформатор) до 3.2-10.Уравнение (13. 57) хорошо описывает эти уравнения Дапона для y +> 30, и вы можете видеть, что доступные данные для малого y +малы и находятся от+ = y *до y * = 5.Области 5 V + 30 достаточно. Это называется переходной зоной, и уравнение 13.
Таким образом, универсальное распределение скорости аналитически представлено уравнением. «+=Г + 0 у + 5; (13.58) И+ = 5.01 n ^ ±3.05 5 y + 30; (13.59) И+ = 2,51 н г/ * + 5.5 30 y +. (13.60) 1; О. Чу. о 0.2 0.4 0.6 0.6 1.0 Рис. 13.7.Смешанный путь[144] как функция расстояния от стены. Приведенные выше рассуждения арепрандтля и т. основаны на исследовании кармана.
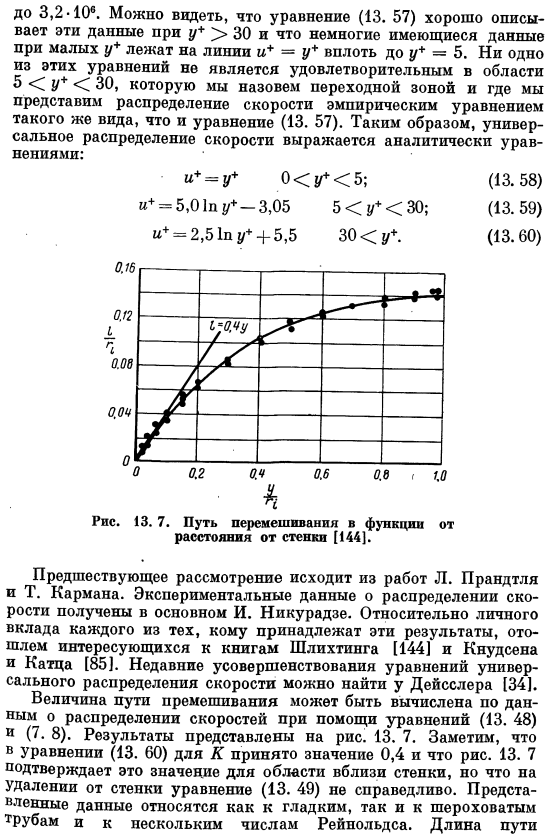
Экспериментальные данные по распределению скоростей в основном получены И. Никурадзе. За личным вкладом каждого человека, владеющего этими результатами, обратитесь к интересующимся книгами Шлихтинга [144] и Кнудсена и Каца [85].Недавнее уточнение универсального уравнения распределения скоростей находится в работе Дайслера [34]. Размер принимающего маршрута определяется по формуле (13. 48) и (7. 8) можно рассчитать по данным о распределении скорости с помощью: результат показан на рисунке. 13.
Формула (13. 60), значение 0,4 используется для K, как показано на рисунке 13. 7 подтверждает это значение в области около стены, но на расстоянии от стены формула (13. 49) является недействительным. Представленная лента связана как с гладкими и грубыми трубами, так и с некоторыми числами Рейнольдса. Длина смешивающего прохода не зависит от обоих факторов, если он достаточно велик. Уравнение скорости движения центра трубы(13. 57) и выглядит так: Сик-Юта » b $ 1 *(13.61) Из этой формулы вытекает формула(13. 57), вы получаете так называемое уравнение скорости или дефицита скорости. itah-я = 41p7 — ’ (13.62) Поскольку K не зависит от шероховатости стенок трубы, формула 13.
Смотрите также:
