Оглавление:
Циркуляция векторного поля
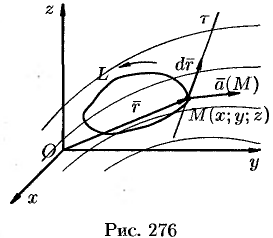
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую  и выберем на ней определенное направление.
и выберем на ней определенное направление.
Пусть 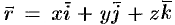 — радиус-вектор точки
— радиус-вектор точки  на контуре
на контуре  . Известно, что вектор
. Известно, что вектор 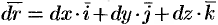 направлен по касательной к кривой в направлении ее обхода (см. рис. 276) и
направлен по касательной к кривой в направлении ее обхода (см. рис. 276) и 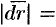
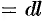 , где
, где 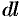 — дифференциал дуги кривой
— дифференциал дуги кривой 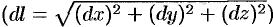 .
.
Криволинейный интеграл по замкнутому контуру  от скалярного произведения вектора
от скалярного произведения вектора  на вектор
на вектор 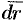 , касательный к контуру
, касательный к контуру  ,
,
называется циркуляцией вектора а вдоль  , т. е.
, т. е.

Рассмотрим различные формы записи циркуляции. Так как
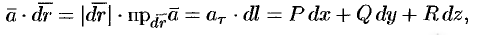
где 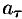 — проекция вектора
— проекция вектора  на касательную
на касательную 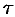 , проведенную в направлении обхода кривой
, проведенную в направлении обхода кривой  , то равенство (71.10) можно записать в виде
, то равенство (71.10) можно записать в виде

или
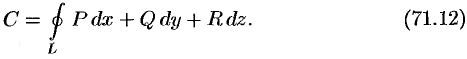
Циркуляция 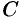 , записанная в виде (71.12) имеет простой физический смысл: если кривая
, записанная в виде (71.12) имеет простой физический смысл: если кривая  расположена в силовом поле, то циркуляция — это работа силы
расположена в силовом поле, то циркуляция — это работа силы 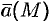 поля при перемещении материальной точки вдоль
поля при перемещении материальной точки вдоль  (п. 56.5).
(п. 56.5).
Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение 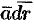 сохраняет знак: положительный, если направление вектора
сохраняет знак: положительный, если направление вектора  совпадает с направлением обхода векторной линии; отрицательный — в противном случае.
совпадает с направлением обхода векторной линии; отрицательный — в противном случае.
Пример №71.5.
Найти циркуляцию вектора ноля линейных скоростей вращающегося тела (см. пример 69.2) 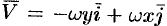 вдоль замкнутой кривой
вдоль замкнутой кривой  , лежащей в плоскости о, перпендикулярной оси вращения.
, лежащей в плоскости о, перпендикулярной оси вращения.
Решение:
Будем считать, что направление нормали к плоскости 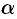 совпадает с направлением оси
совпадает с направлением оси 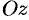 . Согласно формуле (71.12), имеем:
. Согласно формуле (71.12), имеем:
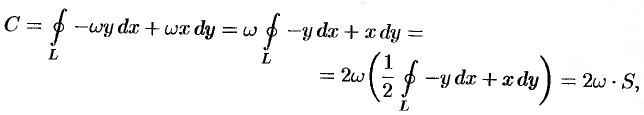
где  — площадь поверхности, ограниченной кривой
— площадь поверхности, ограниченной кривой  (см. 56.17).
(см. 56.17).
Заметим, что если нормаль к поверхности  образует угол
образует угол 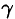 с осью Oz, то циркуляция будет равна
с осью Oz, то циркуляция будет равна 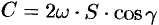 ; с изменением угла
; с изменением угла 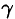 величина
величина 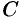 изменяется.
изменяется.
Пример №71.6.
Вычислить циркуляцию векторного поля
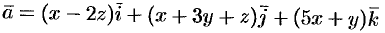
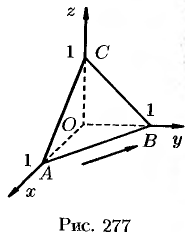
вдоль периметра треугольника с вершинами 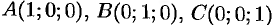 (см. рис. 277).
(см. рис. 277).
Решение:
Согласно формуле (71.12), имеем:
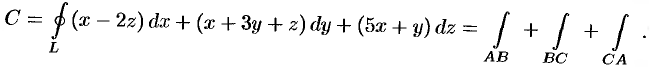
На отрезке 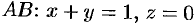 , следовательно,
, следовательно,
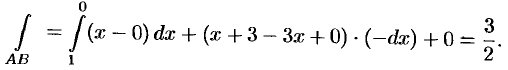
На отрезке 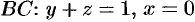 , следовательно,
, следовательно,
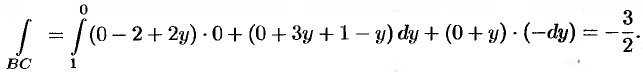
На отрезке 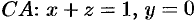 , следовательно,
, следовательно,
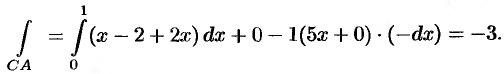
Следовательно,
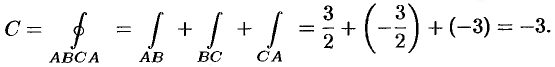
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Градиент скалярного поля и его свойства |
| Дивергенция поля. Формула Остроградского-Гаусса |
| Ротор векторного поля. Формула Стокса |
| Свойства основных классов векторных полей |

