Цилиндрические и конические винтовые линии

Цилиндрические и конические винтовые линии

Из пространственных кривых в технике находят широкое применение винтовые линии и поверхности. Винтовую линию можно рассматривать как результат перемещения точки по поверхности вращения.

Гелисой называют винтовую линию, которая образуется в результате равномерного вращения точки вокруг оси и одновременного перемещения с постоянной скоростью вдоль нее.

Величину 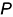перемещения точки вдоль направления оси, соответствующем одному ее обороту вокруг оси, называют шагом винтовой линии.

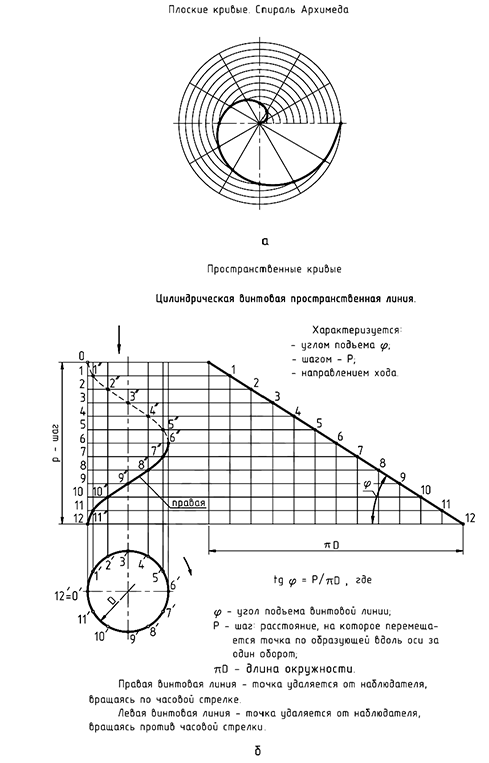
Для построения проекции винтовой линии, в частности гелисы, предварительно строят проекции прямого кругового цилиндра (рис. 11.7, б).

Окружность основания цилиндра (горизонтальная проекция гелисы) делят на равное количество равных частей (например, на 12, так как это можно сделать тем же раствором циркуля, которым была вычерчена окружность). На такое же количество частей делят цилиндр по высоте, равной шагу винтовой линии, на фронтальной проекции. Из точек, отмеченных на окружности, проводят вертикальные линии связи до их пересечения с горизонтальными линиями, проведенными из соответствующих точек деления шага. Соединив полученные точки плавной кривой линией, получают фронтальную проекцию винтовой линии (линия изображена с учетом ее видимости на поверхности цилиндра, рис. 11.7, б).

Различают правые и левые винтовые линии. Изображенная на рис. 11.7, б цилиндрическая винтовая линия является правой. Она характеризуется тем, что при вращении по часовой стрелке точка удаляется от наблюдателя, а при вращении против часовой стрелки — приближается. Если эти условия не соблюдаются, винтовая линия называется левой.

На рис. 11.7, б справа показано построение развертки винтовой линии. Там же приведена формула для определения крутизны винтовой линии.

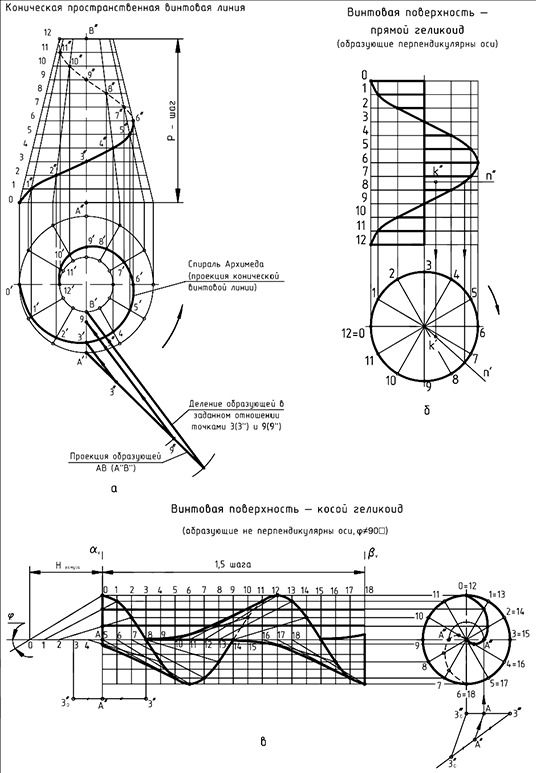
На рис. 11.8, а приведена коническая винтовая линия, которая образуется в результате движения точки по поверхности конуса при условии, что она равномерно вращается вокруг оси конуса и движется вдоль нее с постоянной скоростью. Судя по направлениям этих ее движений — это также правая винтовая линия. Для построения ее проекций горизонтальные проекцию окружностей оснований приведенного усеченного конуса делят на 12 равных частей и, соединяя их, строят горизонтальные проекции образующих конуса.

Определив фронтальные проекции полученных точек посредством линий связей, строят фронтальные проекции образующих. Затем делят конус по высоте (равна шагу винтовой линии) на то же количество частей горизонтальными линиями и отмечают точки их пересечения с фронтальными проекциями образующих.

Соединив найденные точки плавной кривой линией, получают фронтальную проекцию конической винтовой линии (линия изображена с учетом видимости ее на поверхности конуса, рис. 11.8, а). Далее, опуская из этих точек линии связи, отмечают на пересечениях с горизонтальными проекциями соответствующих образующих точки, через которые пройдет горизонтальная проекция конической винтовой линии.

По форме она представляет собой спираль Архимеда. Там же, на рис. 11.8, а, показаны дополнительные построения по определению горизонтальных проекци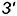й и 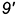точек винтовой линии на образующих, не пересекаемых линиями связи, а сливающихся с ними.

Графически показано, как поделены горизонтальные проекции этих образующих на отрезки в том же отношении, в котором поделены их фронтальные проекции винтовой линией (для уменьшения количества построений указанное деление обоих отрезков совмещено в одном построении).

Винтовые поверхности — прямой и косой геликоиды

При винтовом движении отрезка линии образуются винтовые поверхности. В зависимости от формы образующей линии, винтовые поверхности могут быть линейчатыми и нелинейчатыми. Они находят большое применение в технике, особенно в машиностроении и поэтому заслуживают отдельного внимания.

Все точки образующей при винтовом движении описывают винтовые линии (за исключением точки, находящейся на оси вращения поверхности), каждая из которых может служить направляющей поверхности. Линейчатые винтовые поверхности называют геликоидами. В зависимости от положения образующей относительно оси вращения геликоиды могут быть прямыми (образующая перпендикулярна оси) и косыми (образующая наклонена к оси).

Чертеж прямого геликоида приведен на рис. 11.8,6. Построение его проекций вначале повторяет построения цилиндрической винтовой линии, приведенные на рис. 11.7, б. Но вместо фронтального очерка цилиндра необходимо показать фронтальные проекции образующих винтовой поверхности. Эти проекции представляют собой горизонтальные отрезки, расположенные между осью вращения поверхности и фронтальной проекцией винтовой линии. Фронтальный очерк прямого геликоида образуют указанная винтовая линия, являющаяся проекцией траектории движения внешнего конца образующей, и проекция траектории движения ее внутреннего конца, совпадающая с фронтальной проекцией оси вращения образующей. Направление геликоида определяют так же, как и винтовой линии.

При построении проекций косого геликоида необходимо знать угол наклона его образующей к оси вращения. Эта поверхность имеет более сложный очерк (рис. 11.4).

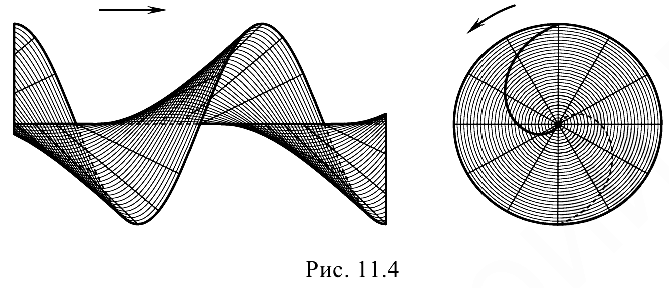
Чертеж косого геликоида, образованного наклонной прямолинейной образующей за 1,5 оборота винтового движения, приведен на рис. 11.5 и повторен на рис. 11.8, в.

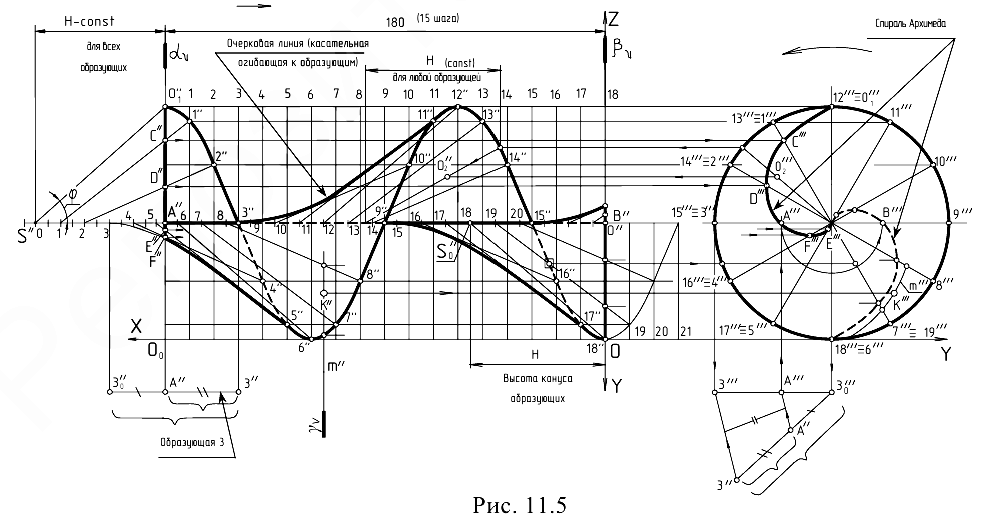
Исходным условием для построений его чертежа является шаг винтового движения образующей и ее начальное положение под углом 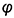к оси вращения (рис. 11.5). В процессе движения образующая должна оставаться параллельной поверхности направляющего конуса высотой 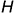. Для построения 18 фронтальных проекций образующей, равномерно расположенных на протяжении 1,5 шага поверхности, используют вспомогательную сетку. При этом расстояние 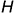между концами каждой образующей, измеренное вдоль оси вращения, должно быть постоянным. Затем проводят огибающие кривые очерковые линии, касательные к проекциям образующих, и строят торцевые срезы рассматриваемого участка косого геликоида профильными плоскостями. Профильные проекции этих срезов представляют собой спирали Архимеда. Проекци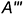и и 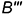точек, принадлежащих образующей в ее третьем и девятом положениях, могут быть определены путем дополнительных построений, основанных на графическом делении отрезков в заданном отношении.

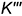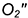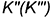Построение недостающей профильной проекции и недостающей фронтальной проекции точек и 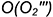, принадлежащих винтовой поверхности, показано на том же чертеже (рис. 11.5). В первом случае использовалась линия 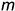сечения поверхности профильной плоскостью 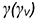, во втором — промежуточная образующая.

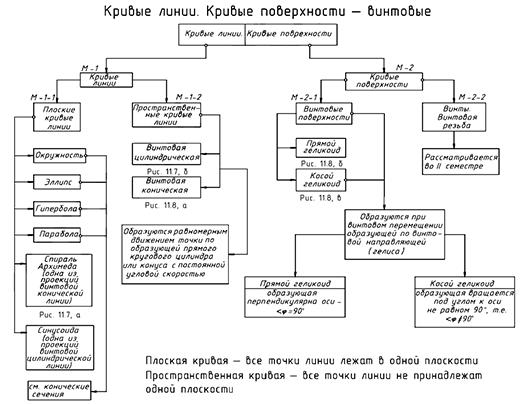
Структуризация материала данной лекции схематически представлена на рис. 11.6 (лист 1). На последующих листах 2 и 3 (рис. 11.7 и 11.8) компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении.

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

 Начертательная геометрия для 1 курса

Возможно эти страницы вам будут полезны:

Кривые линии и поверхности

Плоские и пространственные кривые линии

Пересечение линии с поверхностью

Кривые поверхности