Цепь с идеальной индуктивностью. Реактивная мощность в цепи с индуктивностью
Идеальной называют индуктивность 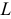 такой катушки, активным сопротивлением
такой катушки, активным сопротивлением 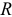 которой можно пренебречь, т. е.
которой можно пренебречь, т. е. 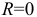 и
и 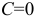 .
.
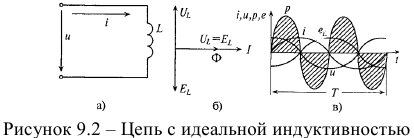
Если в цепи идеальной катушки индуктивностью L (рис. 9.2 а) проходит синусоидальный ток 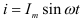 ,то этот ток создает в катушке синусоидальный магнитный поток
,то этот ток создает в катушке синусоидальный магнитный поток 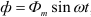 , который индуктирует в катушке ЭДС самоиндукции, равную
, который индуктирует в катушке ЭДС самоиндукции, равную
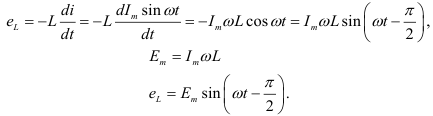
По второму закону Кирхгофа для мгновенных значений можно написать
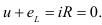
Напряжение, приложенное к цепи с идеальной индуктивностью:
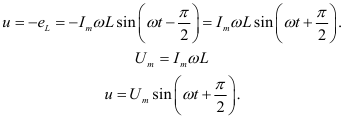
Таким образом, напряжение, приложенное к цепи с идеальной индуктивностью, как и ток в этой цели, изменяется по синусоидальному закону, но опережает ток по фазе на угол 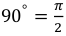 (рис. 9.2 б, в).
(рис. 9.2 б, в).
Закон Ома для этой цепи можно записать иначе: 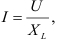 где
где 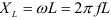
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
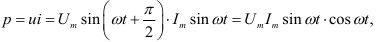
где 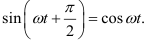
Следовательно, 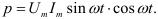
Полученное уравнение умножают и делят на 2: 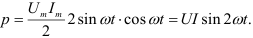
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
На диаграмме (рис. 9.2 в) видно, что мгновенная мощность 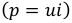 в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой. Такая колеблющая мощность (энергия), в отличии от активной, т.е. потребляемой, называется реактивной.
в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой. Такая колеблющая мощность (энергия), в отличии от активной, т.е. потребляемой, называется реактивной.
Обозначается реактивная мощность буквой 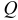 и измеряется в варах, т. е.
и измеряется в варах, т. е. 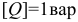 (вольт-ампер реактивный).
(вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
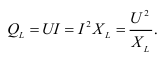
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:

