Центр тяжести однородного тела
Рассмотрим частный случай однородного тела, т. е. тела одинаковой плотности во всех его точках. Обозначая объем элемента тела через объем всего тела через 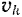 и его удельный вес через
и его удельный вес через 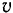 , получим вес элемента тела
, получим вес элемента тела 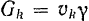 и вес всего тела
и вес всего тела 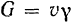 . Подставляя эти значения в первую из формул (42), найдем:
. Подставляя эти значения в первую из формул (42), найдем:
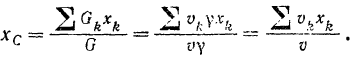
Аналогичные формулы, очевидно, получаются и для двух других координат. Как видно из предыдущего выражения, для однородного тела координаты его центра тяжести не зависят от удельного веса 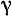 , а зависят лишь от объема, занимаемого данным телом, и его формы.
, а зависят лишь от объема, занимаемого данным телом, и его формы.
Поэтому центр тяжести однородного тела называется центром тяжести объема. Его координаты
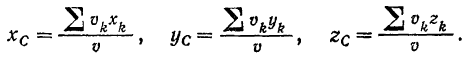
Под 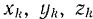 в этих формулах надо понимать координаты центра тяжести элемента тела.
в этих формулах надо понимать координаты центра тяжести элемента тела.
На практике часто приходится определять положение центра тяжести однородных плоских фигур. Такие фигуры можно представлять себе как тонкие однородные пластинки, толщиной которых можно пренебречь. Объемы отдельных частиц такой пластинки пропорциональны площадям соответствующих элементов фигуры, и координаты ее центра тяжести будут зависеть только от площади фигуры и ее формы.
Поэтому центр тяжести однородной тонкой пластинки постоянной толщины, имеющей очертание плоской фигуры, называется центром тяжести площади плоской фигуры.
Его координаты
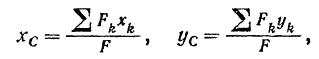
где 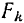 — площадь произвольного элемента фигуры,
— площадь произвольного элемента фигуры, 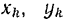 — координаты центра тяжести этого элемента,
— координаты центра тяжести этого элемента, 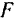 — площадь всей фигуры.
— площадь всей фигуры.
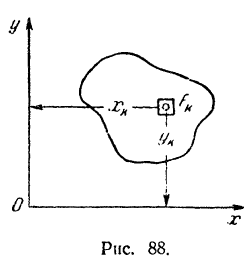
Формулы (44) можно несколько видоизменить. Возьмем произвольную плоскую фигуру (рис. 88) и разобьем ее площадь на отдельные элементы 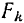 .
.
Сумма, составленная из произведений каждой элементарной площадки данной плоской фигуры на алгебраическое значение ее расстояния до какой-либо оси, называется статическим моментом площади фигуры относительно этой оси.
Обозначая статические моменты площади фигуры относительно координатных осей 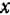 и
и 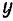 соответственно через
соответственно через 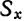 и
и 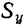 , будем иметь:
, будем иметь:
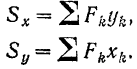
Статический момент площади имеет, очевидно, размерность куба длины, так как представляет собой произведение величины площади, измеряемой в единицах длины в квадрате, на расстояние, измеряемое в единицах длины. Заменяя принятыми обозначениями статических моментов площади числители формул (44), получаем другие выражения для координат центра тяжести плоской фигуры:
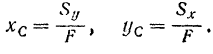
По этим формулам вычисляются координаты центра тяжести плоской фигуры, если известны ее статические моменты относительно координатных осей, и, наоборот, сами статические моменты, если известно положение центра тяжести фигуры.
Если площадь поперечного сечения однородного тела одинакова по всей его длине и поперечные размеры очень малы по сравнению с длиной, то такое тело можно рассматривать как материальную линию. Веса и объемы отдельных частей такого тела будут пропорциональны их длинам, и координаты центра тяжести его будут зависеть лишь от длины и формы этой линии.
Центр тяжести однородного тела, площадь поперечного сечения которого одинакова по всей его длине и мала по сравнению с нею, называется центром тяжести линии.
Его координаты
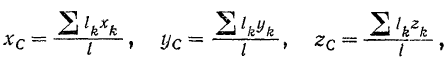
где 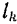 — элемент длины тела,
— элемент длины тела, 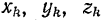 — координаты центра тяжести этого элемента и
— координаты центра тяжести этого элемента и 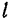 — длина всего тела.
— длина всего тела.
Теорема. Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести его лежит соответственно в плоскости, на оси или в центре симметрии.
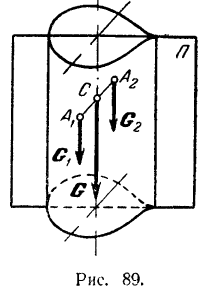
Доказательство. Если тело симметрично относительно некоторой плоскости 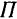 (рис. 89), то каждой частице тела по одну сторону этой плоскости соответствует равная ей по весу и симметрично расположенная частица по другую сторону плоскости.
(рис. 89), то каждой частице тела по одну сторону этой плоскости соответствует равная ей по весу и симметрично расположенная частица по другую сторону плоскости.
Возьмем какую-нибудь частицу 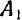 по одну сторону плоскости и найдем симметричную ей частицу
по одну сторону плоскости и найдем симметричную ей частицу 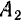 по другую сторону. На эти частицы будут действовать одинаковые по модулю силы тяжести
по другую сторону. На эти частицы будут действовать одинаковые по модулю силы тяжести 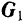 и
и 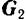 . Равнодействующая
. Равнодействующая 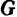 этих двух равных и параллельных сил будет приложена в середине
этих двух равных и параллельных сил будет приложена в середине 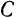 отрезка
отрезка 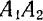 , т. е. в плоскости симметрии.
, т. е. в плоскости симметрии.
Складывая подобным образом силы тяжести каждой пары симметричных частиц, мы получим систему параллельных сил, лежащих в плоскости симметрии тела. В этой же плоскости, очевидно, будет лежать и центр тяжести тела.
Для случаев, когда тело имеет ось или центр симметрии, теорема доказывается совершенно аналогично.
Следствие
- Центр тяжести отрезка материальной прямой линии лежит в его середине.
- Центр тяжести площади параллелограмма лежит в точке пересечения его диагоналей.
- Центры тяжести площадей правильного многоугольника, круга и эллипса и объема шара лежат в их геометрических центрах.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

