Центр параллельных сил
Зная правила сложения двух параллельных сил, нетрудно путем последовательного сложения найти равнодействующую и для любой системы параллельных сил. Пусть, например, к телу приложены в точках 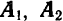 и
и 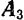 три параллельные и направленные в одну сторону силы
три параллельные и направленные в одну сторону силы 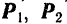 и
и 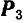 . Сложив сначала две силы
. Сложив сначала две силы
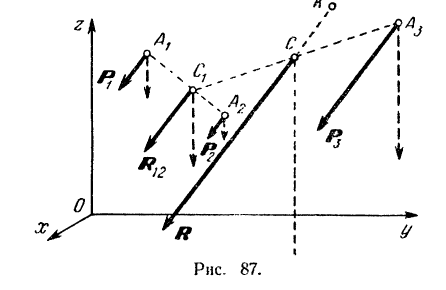
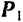 и
и 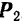 , найдем их равнодействующую
, найдем их равнодействующую 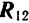 . Она будет параллельна составляющим и направлена в ту же сторону. Модуль ее
. Она будет параллельна составляющим и направлена в ту же сторону. Модуль ее
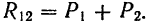
Точка 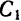 ее приложения определяется из пропорции
ее приложения определяется из пропорции
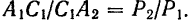
Складывая затем силы 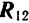 и
и 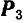 , найдем равнодействующую
, найдем равнодействующую 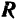 всех трех сил системы. Она будет также параллельна составляющим и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил
всех трех сил системы. Она будет также параллельна составляющим и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил
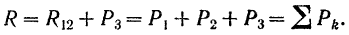
Точка 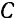 приложения равнодействующей определится из пропорции
приложения равнодействующей определится из пропорции
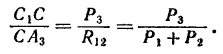
Повернув все силы системы вокруг их точек приложения в одну и ту же сторону на какой-либо одинаковый угол (например, в положения, указанные на рис.87 пунктиром), мы получим новую систему параллельных сил, с темп же модулями и точками приложения составляющих, но с другими линиями действия сил. Последовательно складывая силы новой системы, мы получим, что равнодействующая  равна по модулю сумме модулей составляющих
равна по модулю сумме модулей составляющих  и
и  и им параллельна, т. е. ее линия действия повернется в ту же сторону и на одинаковый угол, что и составляющие. Положение же точки
и им параллельна, т. е. ее линия действия повернется в ту же сторону и на одинаковый угол, что и составляющие. Положение же точки 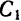 приложения равнодействующей
приложения равнодействующей 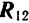 , определяемое из пропорции
, определяемое из пропорции 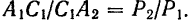 , останется неизменным, так как не изменились ни модули сил, ни отрезок
, останется неизменным, так как не изменились ни модули сил, ни отрезок 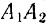 прямой, соединяющий их точки приложения. Рассуждая подобным же образом, найдем, что не изменится и положение точки
прямой, соединяющий их точки приложения. Рассуждая подобным же образом, найдем, что не изменится и положение точки 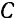 приложения равнодействующей
приложения равнодействующей 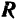 всех сил данной системы.
всех сил данной системы.
Тонка 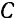 через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах всех сил системы вокруг их точек приложения а одну и ту же сторону и на одинаковый угол, называется центром данной системы параллельных сил.
через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах всех сил системы вокруг их точек приложения а одну и ту же сторону и на одинаковый угол, называется центром данной системы параллельных сил.
За точку приложения равнодействующей 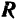 можно принять, конечно, любую точку, лежащую на линии ее действия (например, точку
можно принять, конечно, любую точку, лежащую на линии ее действия (например, точку 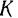 на рис. 87), но только одна из них, именно точка
на рис. 87), но только одна из них, именно точка 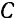 , обладает тем свойством, что через нее всегда проходит равнодействующая данной системы параллельных сил при любом одинаковом их повороте.
, обладает тем свойством, что через нее всегда проходит равнодействующая данной системы параллельных сил при любом одинаковом их повороте.
Выведем теперь формулы для определения координат центра системы параллельных сил. Возьмем пространственную систему осей координат и обозначим координаты точек приложения данных сил: 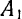 соответственно через
соответственно через 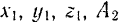 — через
— через 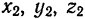 и
и 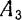 — через
— через 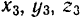 .
.
Координаты центра параллельных сил 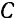 обозначим через
обозначим через 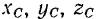 . Вычислим сначала абсциссу
. Вычислим сначала абсциссу 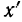 точки
точки 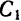 к которой приложена равнодействующая
к которой приложена равнодействующая 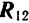 сил
сил 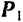 и
и 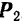 . Воспользуемся для этого известной формулой аналитической геометрии для координат точки, делящей отрезок в данном отношении
. Воспользуемся для этого известной формулой аналитической геометрии для координат точки, делящей отрезок в данном отношении 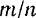 . По этой формуле
. По этой формуле
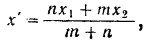
где 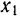 и
и 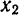 — координаты концов данного отрезка. В нашем случае
— координаты концов данного отрезка. В нашем случае
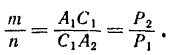
Следовательно,
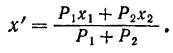
Найдем теперь абсциссу 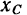 точки
точки 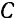 , в которой приложена равнодействующая
, в которой приложена равнодействующая 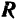 , т. е. абсциссу центра трех данных параллельных сил. Так как
, т. е. абсциссу центра трех данных параллельных сил. Так как
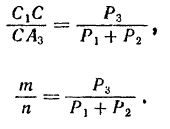
По той же формуле получим:
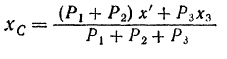
или, подставляя найденное выше для 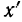 значение,
значение,
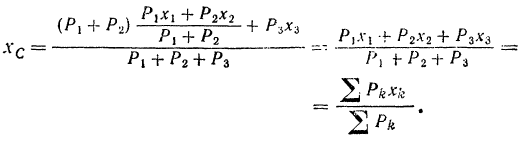
Совершенно аналогично можно найти и другие координаты центра параллельных сил. Таким образом, мы получаем следующие формулы для координат центра системы параллельных сил:
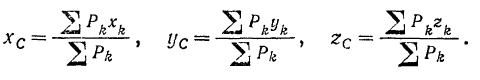
Формулы (41) для координат центра параллельных сил остаются верными при любом числе параллельных сил. Можно доказать, что они верны и для случая, когда в состав системы входят параллельные силы противоположного направления, если только под 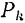 понимать алгебраическое значение силы (со знаком « + » для одного направления сил и со знаком «—» для противоположного) и если только алгебраическая сумма
понимать алгебраическое значение силы (со знаком « + » для одного направления сил и со знаком «—» для противоположного) и если только алгебраическая сумма 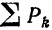 всех сил не равна нулю.
всех сил не равна нулю.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
