Центр масс системы
Каждая точка 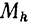 системы имеет определенную массу
системы имеет определенную массу 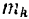 и ее положение определяется в каждый момент времени координатами
и ее положение определяется в каждый момент времени координатами 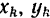 и
и 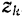 .
.
Центром масс или центром инерции системы называется такая геометрическая точка 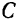 , положение которой определяется в каждый момент времени следующими координатами:
, положение которой определяется в каждый момент времени следующими координатами:
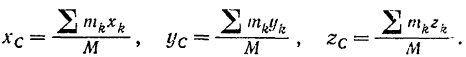
В этих формулах:
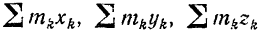
суммы произведений масс точек системы на соответствующие их координаты, 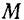 — полная масса системы, равная сумме масс всех точек системы.
— полная масса системы, равная сумме масс всех точек системы.
Если положение центра масс определять радиусом-вектором 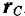 , проведенным в эту точку из начала координат, то из формул (138) следует формула
, проведенным в эту точку из начала координат, то из формул (138) следует формула
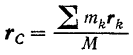
Каждой из формул (138) можно придать другой вид, если умножить числитель и знаменатель ее правой части на ускорение свободного падающего тела. Мы получим
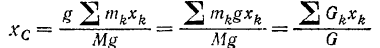
и аналогично
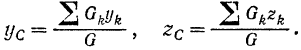
Данными же формулами определяются (формулы (42)) координаты центра тяжести тела.
Для тела не слишком больших размеров центр тя’ жести, как видим, геометрически совпадает с его центром масс. Однако понятия центра тяжести и центра масс не тождественны.
Формулы (42) для координат центра тяжести тела были выведены (§ 38) в предположении, что силы тяжести его частиц параллельны. Степень точности этого допущения зависит, следовательно, от размеров тела. Понятие центра тяжести применимо только к таким системам, которые находятся в однородном поле земного тяготения (в небольших областях вблизи поверхности Земли), и лишено смысла, например, для такой системы как солнечная. Положение Же центра масс, определяемое формулами (138), зависит только от масс точек системы и положения этих точек в рассматриваемый момент времени. Понятие о центре масс сохраняет свой смысл для любой механической системы, независимо от того, какие силы на нее действуют и, следовательно, является более широким понятием, чем понятие о центре тяжести тела.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Вынужденные колебания материальной точки с примером решения |
| Механическая система |
| Момент инерции тела относительно оси |
| Теорема о моментах инерции тела относительно параллельных осей |

