Оглавление:
Целые алгебраические уравнения и неравенства. Линейные уравнения и неравенства
Уравнение вида

где а и b — коэффициенты (действительные числа или выражения, зависящие от параметров), а x — неизвестное, называется линейным уравнением. Если b = 0 , то линейное уравнение называется однородным.
Общая схема решения линейного уравнения 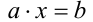 подразумевает возможность реализации трёх случаев.
подразумевает возможность реализации трёх случаев.
1) Если 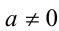 , то уравнение имеет единственное решение
, то уравнение имеет единственное решение 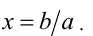
2) Если а = 0 и b = 0 , то уравнение имеет бесконечно много решений (любое действительное x будет являться решением).
3) Если 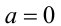 и
и 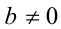 , то уравнение не имеет решений.
, то уравнение не имеет решений.
Пример №147.
При всех значениях а решить уравнение 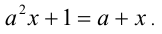
Решение:
Приведём для начала данное линейное уравнение к стандартному виду:

и воспользуемся предложенной схемой решения. Если 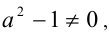 т.е.
т.е. 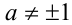 , то уравнение для каждого такого а имеет единственное решение
, то уравнение для каждого такого а имеет единственное решение 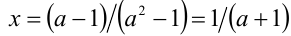 . Если а = 1, то, подставляя это значение параметра в (2), получим уравнение 0 • x = 0 , решением которого, очевидно, является любое действительное число x . Если же а = — 1, то уравнение (2) приобретает вид 0 • X = — 2 и, очевидно, не имеет решений.
. Если а = 1, то, подставляя это значение параметра в (2), получим уравнение 0 • x = 0 , решением которого, очевидно, является любое действительное число x . Если же а = — 1, то уравнение (2) приобретает вид 0 • X = — 2 и, очевидно, не имеет решений.
Ответ: при 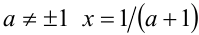 ; при
; при 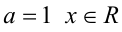 ; при
; при 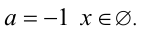
Иногда задача формулируется не в общем виде, т.е. «при всех значениях параметра решить линейное уравнение…», когда в процессе решения надо рассматривать все три возможных случая, а в более узкой постановке. Например, «найти значения параметра, при которых линейное уравнение имеет единственное решение», или «найти значения параметра, при которых линейное уравнение не имеет решений».
Запомним, что линейное уравнение 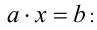
1) имеет единственное решение 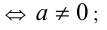
2) не имеет решений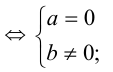
3) имеет бесконечно много решений 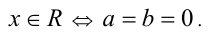
Пример №148.
При каких значениях параметра b уравнение
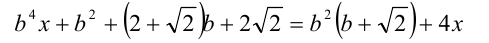
имеет бесконечно много корней?
Решение:
Относительно неизвестной x это линейное уравнение. Приведём его вначале к виду (1):
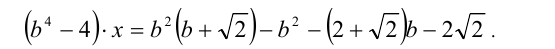
Выпишем необходимое и достаточное условие того, что это уравнение имеет бесконечно много решений:
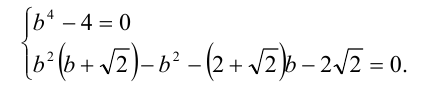
Очевидно, первому уравнению в системе удовлетворяют два различных действительных корня 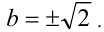 Проверим, удовлетворяют ли они второму уравнению системы. Успешную проверку проходит только корень
Проверим, удовлетворяют ли они второму уравнению системы. Успешную проверку проходит только корень 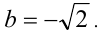
Пример №149.
При каких значениях параметров а и b уравнение
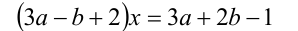
имеет единственное решение?
Решение:
Необходимым и достаточным условием того, что данное уравнение имеет единственное решение, является необращение в нуль старшего коэффициента: 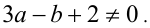 Учитывая, что равенству
Учитывая, что равенству 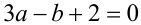 удовлетворяет бесконечное множество пар чисел вида
удовлетворяет бесконечное множество пар чисел вида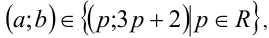 и что множество всевозможных пар действительных чисел а и b обозначается
и что множество всевозможных пар действительных чисел а и b обозначается
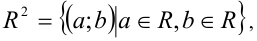
приходим к выводу, что искомое множество пар — это вся координатная плоскость Оаb, из которой удалены точки, лежащие на прямой b = За + 2 .
Ответ: 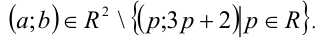
Неравенства вида 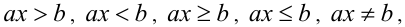 где а и b -действительные числа или выражения, зависящие от параметров, а x — неизвестное, называются линейными неравенствами.
где а и b -действительные числа или выражения, зависящие от параметров, а x — неизвестное, называются линейными неравенствами.
Рассмотрим в общем виде решение линейного неравенства
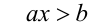
(неравенства 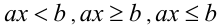 решаются аналогично). Возможны следующие случаи.
решаются аналогично). Возможны следующие случаи.
1) Если а > 0 , то решением неравенства будет промежуток x > b/а .
2) Если а < 0, то решением неравенства будет промежуток x < b/а .
3) Если а = 0 и b < 0, то неравенство имеет бесконечно много решений (любое действительное x является решением); если 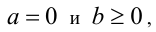 то неравенство не имеет решений.
то неравенство не имеет решений.
Пример №150.
Решить при всех значениях параметра а неравенство
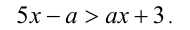
Решение:
Приведём данное линейное относительно x неравенство к виду

Если 5 — а > 0, т.е. а < 5 , то, поделив на 5 — а , получим х > (а + 3)/(5 — а); если 5-а < 0, т.е. а > 5 , то, поделив на 5 — а , получим x < (а + 3)/(5-a).
Наконец, если а = 5, то, подставляя это значение параметра в неравенство (3), получаем неравенство 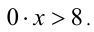 Очевидно, оно не имеет решений.
Очевидно, оно не имеет решений.
Пример №151.
При каких значениях параметров а и b неравенство
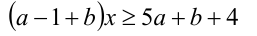
а) не имеет решений; б) имеет бесконечно много решений?
Решение:
а) Неравенство не имеет решений тогда и только тогда, когда
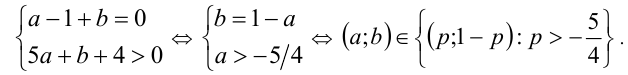
б) В остальных случаях неравенство имеет бесконечно много решений, поэтому получаем ответ:
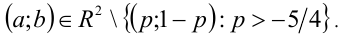
Пример №152.
При каких значениях параметра а решением неравенства
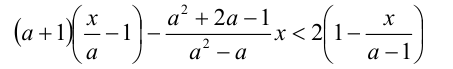
является любое 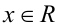 ?
?
Решение:
ОДЗ: 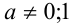 . Так как неравенство линейно относительно переменной x, то, приведя его к стандартному виду, получим
. Так как неравенство линейно относительно переменной x, то, приведя его к стандартному виду, получим
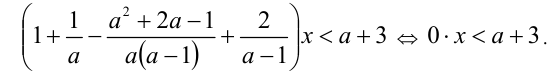
Теперь видно, что любое действительное число x будет решением этого неравенства только при а > — 3 . С учётом ОДЗ приходим к ответу.
Ответ: при 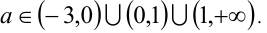
Наконец, рассмотрим, как решается в общем виде линейное неравенство вида
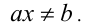
1) Если 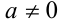 , то решением неравенства будет
, то решением неравенства будет 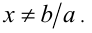
2) Если а = 0 и b = 0 , то неравенство не имеет решений.
3) Если 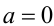 и
и 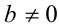 ,то неравенство выполняется сразу для всех действительных значений переменной x.
,то неравенство выполняется сразу для всех действительных значений переменной x.
Пример №153.
Решить неравенство при всех значениях параметра а
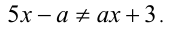
Решение:
Приведём неравенство к стандартному виду:
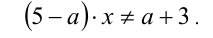
Если 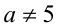 , то решением неравенства будет объединение промежутков
, то решением неравенства будет объединение промежутков 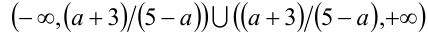 . Если а= 5, то неравенство примет вид
. Если а= 5, то неравенство примет вид 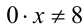 , что верно при всех
, что верно при всех 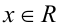 .
.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
| Примеры равносильных преобразований |
| Примеры неравносильных преобразований в математике с примерами решения |
| Квадратные уравнения и неравенства |
| Формула корней квадратного уравнения |

