Оглавление:
Целочисленное линейное программирование
Рассмотрим следующую задачу линейного программирования: максимизировать
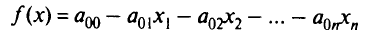
при условии
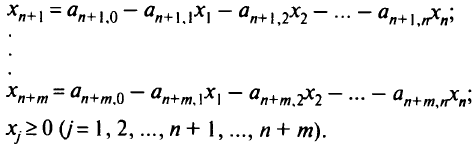
Заметим, что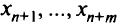 
— слабые переменные, а 
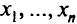— исходные переменные задачи (2.5). Если наряду с ограничениями (2.5) потребовать, чтобы все 
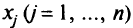были целыми, то задача будет называться задачей целочисленного программирования. Существует большое число задач, особенно комбинаторных, которые можно сформулировать как задачи целочисленного программирования.
Ограничения (2.5) определяют выпуклую область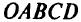 
в 
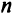-мерном пространстве, как показано на рис. 2.6. Узлы целочисленной решетки на рис. 2.6 изображены точками. Такие точки, расположенные внутри области 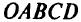, являются допустимыми решениями задачи целочисленного программирования. Оптимальные решения задачи линейного программирования всегда располагаются на границе области решений. В данном случае граничные точки не являются даже допустимыми решениями, поскольку ни одна из них не целочисленна.
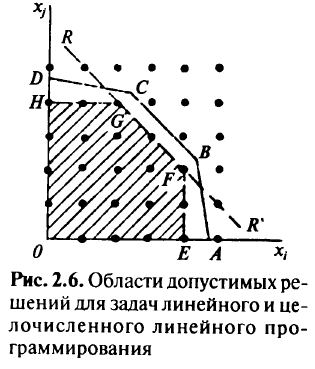
Предположим, что область допустимых решений сужена до выпуклой оболочки допустимых целых точек внутри допустимой области. На рис. 2.6 эта выпуклая оболочка показана затененной областью 
, которую можно рассматривать как область допустимых решений некоторой другой задачи линейного программирования.
Действительно, если к задаче линейного программирования, определяющей допустимую область , добавить ограничение типа 
, как показано на рис. 2.6, то для вновь полученной задачи 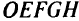будет областью допустимых решений. Такая область обладает двумя важными свойствами: 1) содержит все допустимые целочисленные точки исходной задачи линейного программирования (поскольку является выпуклой оболочкой этих точек); 2) все крайние точки новой области — целочисленны. Поэтому любое базисное оптимальное решение модифицированной задачи линейного программирования имеет своими компонентами целые числа и является оптимальным решением исходной задачи целочисленного программирования.
Как только будут введены дополнительные ограничения, можно решать модифицированную задачу линейного программирования любым обычным методом, и полученное базисное оптимальное решение автоматически будет целочисленным. Представленный ниже целочисленный алгоритм обладает следующими свойствами: 1) все дополнительные ограничения сохраняют допустимые точки исходной целочисленной задачи; 2) за конечное число шагов создается достаточное число дополнительных ограничений для того, чтобы оптимальное решение модифицированной задачи было целочисленным; 3) дополнительные ограничения (гиперплоскости) проходят по крайней мере через одну целочисленную точку, хотя и не обязательно находящуюся внутри выпуклой оболочки; 4) каждое новое ограничение сокращает область допустимых решений исходной задачи целочисленного программирования.
Следует подчеркнуть, что оптимальное решение исходной задачи может быть получено прежде, чем размер допустимой области будет сокращен до размеров выпуклой оболочки. К тому же, поскольку оптимальное целочисленное решение определяется пересечением гиперплоскостей, таких гиперплоскостей существует не более, чем это необходимо; некоторые из них могут соответствовать ограничениям исходной задачи.
Задачу целочисленного программирования также можно записать в виде табл. 2.14.
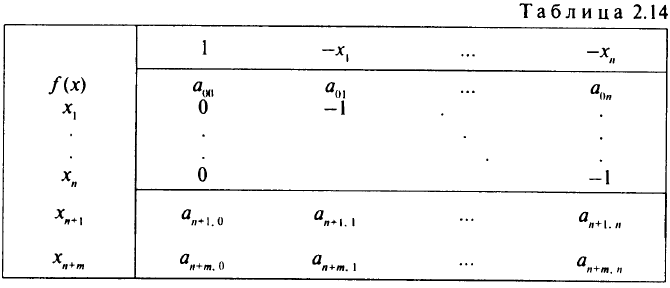
Обычно в ограничения задачи (2.5) включают тривиальные соотношения
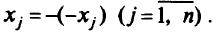
Причины представления переменных в виде
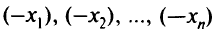
чисто исторические, но это стало практикой в целочисленном программировании. Будем использовать
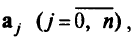
для обозначения 
-го столбца те кущей таблицы и
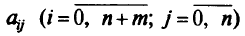
для обозначения элемента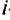 
-й строки и 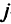-го столбца таблицы. Предполагается, что все 
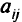в исходной таблице целые. Следовательно, все слабые переменные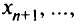 
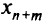должны быть также неотрицательными целыми числами.
Вначале задачу целочисленного программирования рассматривают как задачу линейного программирования и решают ее с помощью прямого или двойственного симплекс-метода. В двойственном симплекс-методе сначала выбирается переменная, которую исключают из базиса. Она определяется наибольшим по модулю отрицательным элементом столбца сводных членов, т.е. не надо решать вспомогательную задачу. Чтобы определить переменную, вводимую в базис, рассматривают отношение элементов строки для целевой функции и соответствующих отрицательных элементов ведущей строки. Наименьшее по значению отношение (в задаче максимизации) определяет переменную, вводимую в базис. Операция замещения проводится методом Жордана. В конце работы алгоритма
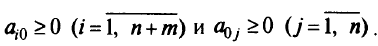
Если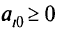 
целые для всех 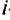, то получено оптимальное решение целочисленной задачи. В этом случае решение получается сразу, без использования ограничений целочисленности. Если 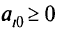, целые не для всех 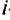, тогда к ограничениям (2.5) добавляют еще одно. Новое ограничение записывают внизу таблицы так, чтобы задача перестала быть прямо допустимой, т.е. 
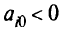для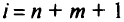 
. Затем используют двойственный симплекс-метод с целью сделать все 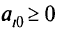. Если 
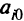получаются нецелыми, в таблицу добавляют новые ограничения до тех пор, пока все 
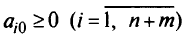не станут целыми и неотрицательными.
Если после введения дополнительного ограничения текущая таблица перестает быть прямо допустимой, то текущее решение, представляющее собой вершину многогранника решений, не удовлетворяет этому дополнительному ограничению. Другими словами, дополнительное ограничение отсекает часть пространства решений. Если дополнительные ограничения не отсекают ни одной целочисленной точки пространства решений исходной задачи, то, вполне вероятно, после введения достаточного числа дополнительных ограничений вершины суженного множества решений будут целочисленными. Тогда, использовав симплекс-метод, можно найти оптимальное целочисленное решение. Трудность состоит в систематическом получении дополнительных ограничений и доказательстве конечности алгоритма.
Каждый раз после проведения итерации симплекс-метода происходит изменение множества небазисных переменных. Изменяется и таблица. Будем использовать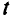 
для обозначения 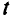-таблицы. Изложим сам алгоритм.
Шаг 1. Решить задачу целочисленного программирования как задачу линейного программирования с помощью прямого или двойственного симплекс-метода. Если получено оптимальное решение задачи линейного программирования, то
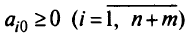
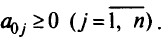
Шаг 2. Если 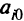— все целые, то задача решена и решение получено без использования дополнительных ограничений. В противном случае пусть 
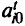— первая нецелочисленная компонента в 
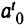. Тогда 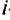-я строка называется производящей. Записать внизу таблицы уравнение, используя данные производящей строки:
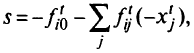
где
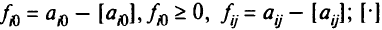
ближайшее к числу целое.
Переменную 5 называют слабой переменной Гомори, а уравнение (2.6) — отсечением Гомори. Проделать шаг (двойственного) симплекс-метода, использовав в качестве ведущей строки отсечение Гомори (2.6). При этом таблица останется двойственно допустимой. Повторять до тех пор, пока все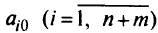 
не станут целыми неотрицательными. Если 
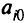на некотором шаге остается отрицательным, следующий шаг (двойственного) симплекс-метода производится без введения отсечения Гомори. (Если 
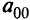становится отрицательным, нулевую строку не выбирают в качестве производящей. Если 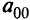становится нецелым, следует выбрать нулевую строку в качестве производящей.)
В приведенном ниже числовом примере все дополнительные ограничения сохраняются на протяжении вычислений.
Это сделано для того, чтобы показать, что эти дополнительные ограничения представляют собой неравенства. Причем, если эти неравенства выразить через исходные небазисные переменные, они будут иметь целые коэффициенты.
Если сохранять все строки, соответствующие слабым переменным Гомори, то эти слабые переменные могут стать базисными. Если слабая переменная Гомори вошла в базис с неотрицательным значением, то соответствующая строка представляет собой неравенство, справедливое при текущем решении, и эта строка может быть вычеркнута. Если слабая переменная Гомори становится базисной с отрицательным значением, соответствующую строку следует использовать в качестве ведущей. Если сохранять все строки, соответствующие всем отсечениям Гомори, то, вообще говоря, потребуется меньшее число дополнительных ограничений, однако увеличение таблицы предпочтительнее, чем введение лишних дополнительных ограничений. Приведем пример, иллюстрирующий алгоритм.
Пример:
Рассмотрим задачу целочисленного программирования:
максимизировать
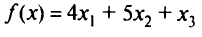
при условиях
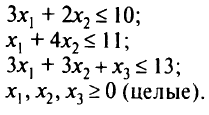
Вводя слабые переменные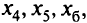 
получаем:
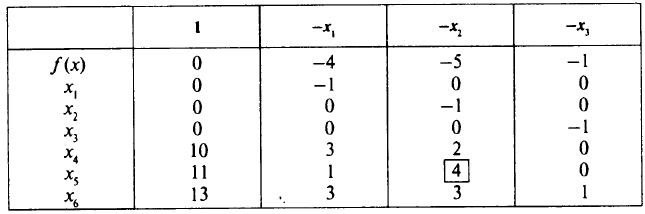
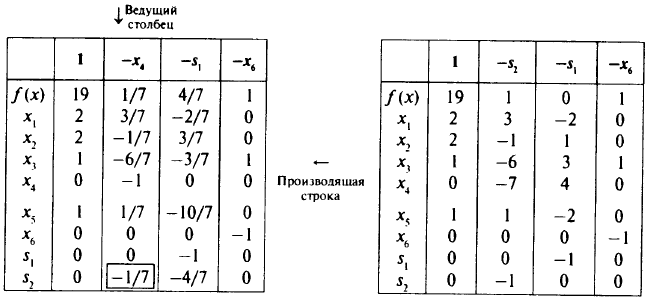
Решаем задачу линейного программирования (ведущий элемент отмечен):
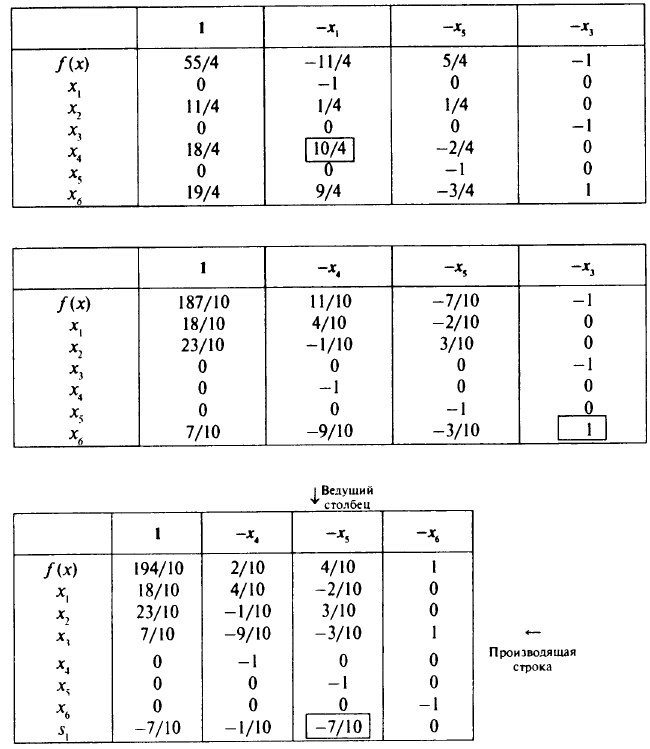
Получено оптимальное решение задачи линейного программирования:
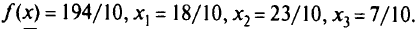
Оно не целочисленное. Приступаем к шагу 2, дописываем в последней таблице уравнение отсечения и назначаем производящую строку и ведущий столбец:
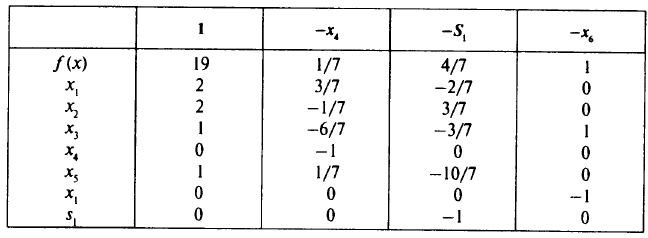
Отсюда находим оптимальное целочисленное решение:
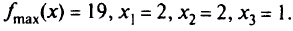
Выразив через исходные небазисные переменные 
и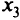 
, получим неравенство 
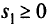целыми коэффициентами:
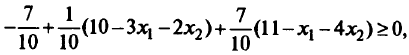
или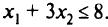 
Чтобы получить матрицу, полностью целочисленную, просто продолжим введение отсечений:
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
