Оглавление:
Целевое программирование
Целевое программирование (ЦП) зародилось как приложение обычного линейного программирования. В настоящее время — это область многокритериальной оптимизации. В целевом программировании устанавливается некоторый уровень достижения целей по каждому критерию. От обычного линейного программирования ЦП отличается следующими особенностями:
1) пониманием критериев как целей;
2) приписыванием приоритетов и/или весов достижению отдельных целей;
3) присутствием переменных 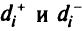 , являющихся мерой отклонения от целевых уровней
, являющихся мерой отклонения от целевых уровней 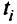 сверху и снизу соответственно;
сверху и снизу соответственно;
4) минимизацией взвешенных сумм переменных отклонений с целью найти решения, наилучшим образом удовлетворяющие целям.
Обычноточка, удовлетворяющая сразу всем целям, не является допустимой. Поэтому стремятся найти допустимую точку, которая достигает всех целей «наилучшим» образом. Для каждой цели (целевой функции) устанавливается значение критерия 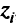 который должен быть достигнут (если возможно) по отношению к обусловленным числами
который должен быть достигнут (если возможно) по отношению к обусловленным числами 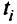 целям.
целям.
В задачах ЦП рассматриваются два утопических множества: 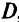 в пространстве решений — множество тех точек из
в пространстве решений — множество тех точек из 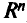 , в которых одновременно достигаются все цели, и
, в которых одновременно достигаются все цели, и 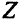 в пространстве критериев — множество критериальных векторов в
в пространстве критериев — множество критериальных векторов в 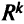 , которые одновременно удовлетворяют всем целям. Необходимо найти точку из
, которые одновременно удовлетворяют всем целям. Необходимо найти точку из 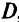 , для которой критериальный вектор — наилучший по сравнению с утопическим множеством
, для которой критериальный вектор — наилучший по сравнению с утопическим множеством 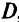 в пространстве критериев.
в пространстве критериев.
В ЦП используются два основных подхода к решению задач: архимедова модель и модель с приоритетами. В архимедовой модели точки-кандидаты в решение генерируются путем определения тех точек из 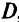 , критериальные вектора которых являются ближайшими в смысле взвешенной метрики в
, критериальные вектора которых являются ближайшими в смысле взвешенной метрики в 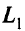 к утопическому множеству в пространстве критериев. Для модели с приоритетами генерируют решения, для которых критериальные вектора оказываются наиболее соответствующими в лексикографическом смысле точками утопического множества в пространстве критериев.
к утопическому множеству в пространстве критериев. Для модели с приоритетами генерируют решения, для которых критериальные вектора оказываются наиболее соответствующими в лексикографическом смысле точками утопического множества в пространстве критериев.
Пример:
Рассмотрим задачу ЦП:
Цели
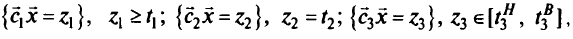
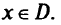
Архимедова формулировка этой задачи имеет вид
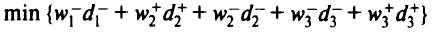
при целевых ограничениях
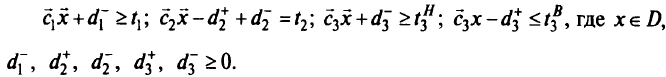
Здесь переменные w в целевой функции — положительные штрафные веса; каждая цель порождает одно целевое ограничение, кроме случая, когда задан диапазон и возникают два целевых ограничения. В формулировке задачи используются переменные отклонений
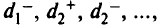
которые соответствуют нежелательным отклонениям.
Архимедова целевая функция представляет собой взвешенную сумму переменных нежелательных отклонений. Переменные w позволяют штрафовать нежелательные отклонения от цели с разной степенью жесткости. Целевые ограничения расширяют область допустимых решений, переводя 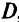 в пространство большей размерности и создавая, таким образом, архимедову область допустимых решений для задачи ЦП.
в пространство большей размерности и создавая, таким образом, архимедову область допустимых решений для задачи ЦП.
Архимедовы задачи ЦП можно решать, используя обычные методы линейного программирования. Но тогда мы можем получить только крайние точки допустимой области в пространстве решений (т.е. крайние точки области 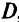 после ее усечения целевыми ограничениями). Возможны следующие варианты таких точек:
после ее усечения целевыми ограничениями). Возможны следующие варианты таких точек:
1) крайние точки области 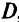 ;
;
2) точки границы области 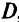 , не являющиеся крайними;
, не являющиеся крайними;
3) внутренние точки области 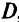 .
.
Если Л П Р предпочитает точку, не являющуюся крайней точкой допустимой области архимедовой задачи ЦП, то ее нельзя определить, не используя процедуры изменения целевых показателей
Задача ЦП с приоритетами. В приоритетном (лексикографическом) ЦП цели группируются по приоритетам. Цели с высшим уровнем приоритета считаются бесконечно важными по сравнению с целями со следующим уровнем приоритета. Рассмотрим задачу ЦП с приоритетами вида
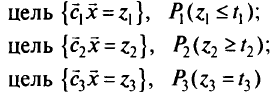
при 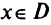 . Здесь для каждой цели указан приоритет
. Здесь для каждой цели указан приоритет
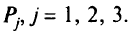
Величины 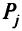 служат и в качестве факторов приоритетов, причем
служат и в качестве факторов приоритетов, причем 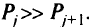
Запишем задачу ЦП с приоритетами в следующей лексикографической форме:
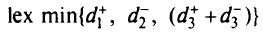
при ограничениях
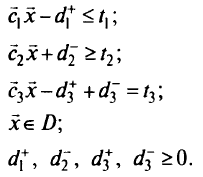
Оптимизация (минимизация) этой задачи осуществляется с помощью алгоритмов линейного программирования. На первом этапе решаем задачу
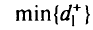
при ограничениях
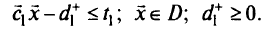
Если в этой задаче есть альтернативные оптимумы, то решаем задачу второго этапа:
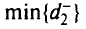
при ограничениях
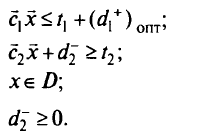
Здесь 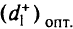 — оптимальное значение переменной
— оптимальное значение переменной 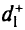 , найденное на первом этапе.
, найденное на первом этапе.
Если в задаче второго этапа есть альтернативные оптимумы, то решаем задачу третьего этапа:
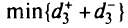
при ограничениях
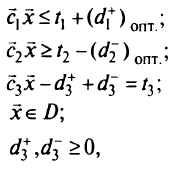
где 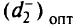 — оптимальное значение
— оптимальное значение 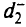 после второго этапа.
после второго этапа.
Любое решение задачи третьего этапа определяет лексикографический минимум в задаче ЦП с приоритетами.
Норешение прекращается, как только на каком-то этапе будет единственное решение, т.е. цели нижних уровней могут и не повлиять на решение.
Задачу ЦП с приоритетами можно решить в одном этапе, использовав лексикографический симплекс -метод.
Пример:
Рассмотрим задачу ЦП с приоритетами вида:
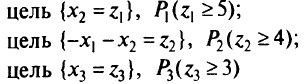
при ограничениях
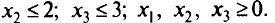
Эта задача преобразуется к виду
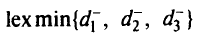
при ограничениях
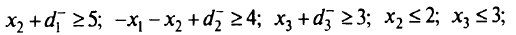
все переменные 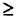 0.
0.
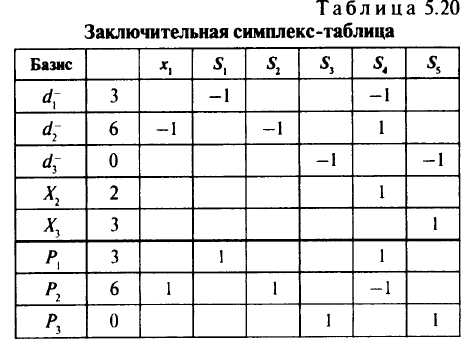
Введем дополнительные переменные 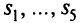 и заполним симплекс-таблицу (табл. 5.19), из которой удалим столбцы базисных переменных;
и заполним симплекс-таблицу (табл. 5.19), из которой удалим столбцы базисных переменных; 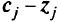 — строка относительных оценок целевой функции для каждого лексикографического уровня
— строка относительных оценок целевой функции для каждого лексикографического уровня 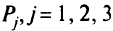 (последние три строки симплекс-таблицы). Нулевые клетки — пустые.
(последние три строки симплекс-таблицы). Нулевые клетки — пустые.
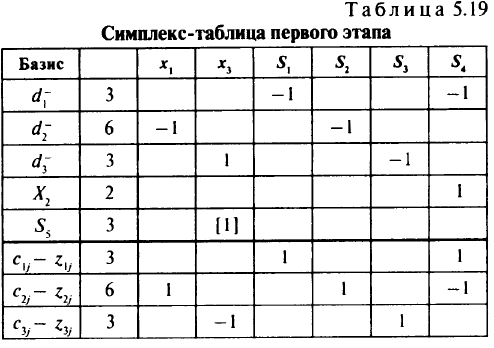
Анализируя строки 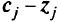 , видим, что переменную
, видим, что переменную 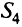 можно было бы перевести в базисные переменные. Тогда целевая функция второго лексикографического уровня может быть уменьшена, но при этом увеличится целевая функция первого лексикографического уровня, чего допустить нельзя. Таким образом, точка
можно было бы перевести в базисные переменные. Тогда целевая функция второго лексикографического уровня может быть уменьшена, но при этом увеличится целевая функция первого лексикографического уровня, чего допустить нельзя. Таким образом, точка 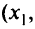
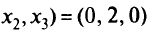 минимизирует целевые функции первого и второго этапов. Так как существуют альтернативные оптимумы, переходим к третьему этапу. Вводим в базис переменную
минимизирует целевые функции первого и второго этапов. Так как существуют альтернативные оптимумы, переходим к третьему этапу. Вводим в базис переменную 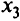 , поскольку в первой и второй строках
, поскольку в первой и второй строках 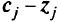 над -1 нет положительных элементов. Получим новую табл. 5.20 и оптимальное решение
над -1 нет положительных элементов. Получим новую табл. 5.20 и оптимальное решение 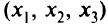 = (0, 2, 3), что и является лексикографическим минимумом для рассматриваемой задачи. В точке оптимального решения для первой цели отклонение
= (0, 2, 3), что и является лексикографическим минимумом для рассматриваемой задачи. В точке оптимального решения для первой цели отклонение 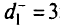 ; для второй цели —
; для второй цели — 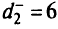 ; третья цель достигнута:
; третья цель достигнута: 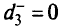 .
.
Наилучшие результаты в решении задач ЦП получаются в интерактивном режиме, когда решаются одновременно обе задачи: архимедова и с приоритетами.
Полезно бывает применить прием масштабирования целевых ограничений — записать отклонения от целей в процентах, т.е. ввести вместо 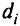 выражение
выражение 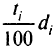 Если дополнительно минимизировать новую переменную
Если дополнительно минимизировать новую переменную 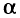 и добавить условие
и добавить условие 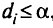 , то такая процедура будет минимизировать максимальное отклонение. В этом случае число дополнительных ограничений равно числу переменных отклонения на рассматриваемом уровне приоритета.
, то такая процедура будет минимизировать максимальное отклонение. В этом случае число дополнительных ограничений равно числу переменных отклонения на рассматриваемом уровне приоритета.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

