Оглавление:
Целая, дробная части действительного числа и их свойства
Теперь, когда сформулировано понятие действительного числа, можно ввести ещё два связанных между собой понятия, характеризующих данное действительное число — его целую и дробную части. Определения целой и дробной частей имеют словесно-описательную форму.
Целой частью действительного числа x называется наибольшее целое число, не превосходящее x, и обозначается [х]. Дробной частью действительного числа x называется разность между самим числом и его целой частью, т.е. x -[х], и обозначается {x}. Например: [5,12] = 5, {5,12} = 0,12; [—5,12] = —6, {-5,12}= 0,88; 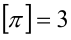 ,
,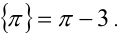
Из определений целой и дробной частей вытекают их основные свойства. Рассмотрим их. Пусть x ,у — произвольные действительные числа, n — любое целое число. Тогда справедливы следующие утверждения.
Свойства целой и дробной частей
1. Целая часть любого действительного числа x есть целое число:
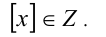
2. Любое действительное число x можно представить в виде суммы его целой и дробной частей, т.е.
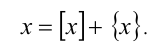
3. Любое действительное число x всегда заключено между своей целой частью (с которой может совпадать) и числом, на единицу большим целой части, т.е.
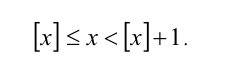
4. Дробная часть любого действительного числа x может принимать значения в пределах от 0 (наименьшее возможное значение) до 1 (это значение не достигается ни при каком x), т.е.
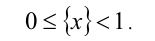
5. Любое целое число n можно выносить (или вносить) из-под знака целой части, т.е.
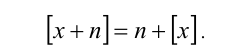
Добавление (или вычитание) к действительному числу x произвольного целого числа n не изменяет значения его дробной части, т.е.
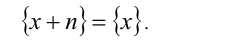
6. Целая часть суммы двух действительных чисел не меньше суммы их целых частей, т.е.
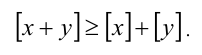
Докажем, например, последнее свойство:
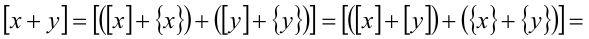
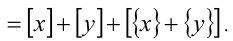 Поскольку
Поскольку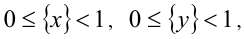 то
то 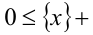
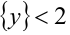 и, следовательно,
и, следовательно, 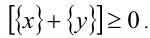 Исполь-зуя последнюю оценку, получаем окончательно необходимый результат:
Исполь-зуя последнюю оценку, получаем окончательно необходимый результат:
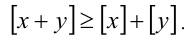
7. Дробная часть суммы двух действительных чисел не больше суммы их дробных частей, т.е.
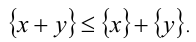
Доказательство. Воспользуемся предыдущим свойством:
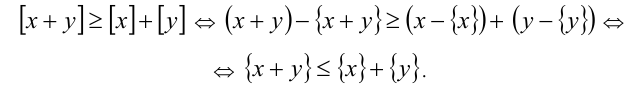
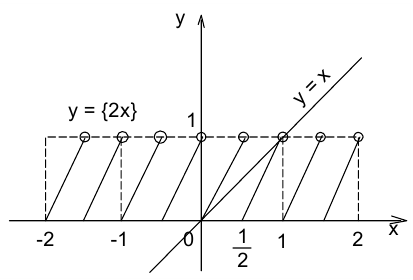
Для построения графиков функций 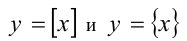 следует разбить всю числовую прямую на полуинтервалы вида
следует разбить всю числовую прямую на полуинтервалы вида 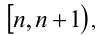 где n — произвольное целое число, и затем рассмотреть поочерёдно каждый из этих промежутков. Это делается потому, что на каждом из указанных промежутков можно однозначно раскрыть целую и дробную части, выписав их значения в явном виде.
где n — произвольное целое число, и затем рассмотреть поочерёдно каждый из этих промежутков. Это делается потому, что на каждом из указанных промежутков можно однозначно раскрыть целую и дробную части, выписав их значения в явном виде.
Так, на полуинтервалах вида 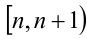 имеем:
имеем: 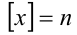 , поэтому график функции
, поэтому график функции 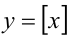 на этих участках совпадает с горизонтальной прямой у = n .
на этих участках совпадает с горизонтальной прямой у = n .
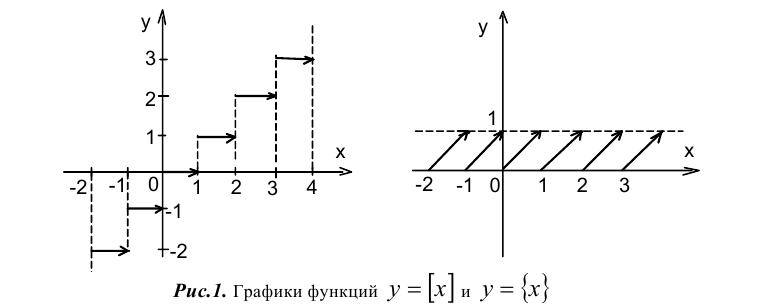
Далее, на рассматриваемом промежутке 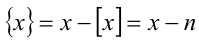 , что означает, что график функции у = {x } совпадает с прямой у = x — n . Объединяя построенные участки графиков, получаем оба искомых графика.
, что означает, что график функции у = {x } совпадает с прямой у = x — n . Объединяя построенные участки графиков, получаем оба искомых графика.
Видно, что обе функции терпят разрывы в виде конечных скачков значений при целочисленных значениях аргумента x. Дробная часть к тому же является периодической функцией с периодом, равным единице. Данные функции не относят к классу элементарных функций.
Заметим, что данный подход, основанный на разбиении числовой прямой на отдельные промежутки, на каждом из которых значения целой и дробной частей можно посчитать, используется и при решении других задач на эту тему, в частности при решении уравнений. В экзаменационных вариантах задачи на свойства целой и дробной частей встречаются достаточно редко и в основном на математических факультетах, однако надо быть готовым к решению задач такого рода.
Пример №101.
Решить неравенство
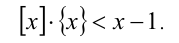
Решение:
Заменим x в правой части неравенства на сумму [х] + {х} :
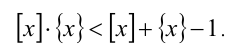
Приведём неравенство к виду 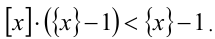 Расклады-вая множители, получаем
Расклады-вая множители, получаем 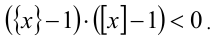 Поскольку
Поскольку 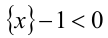 , то неравенство оказывается равносильно неравенству
, то неравенство оказывается равносильно неравенству решая которые находим
решая которые находим 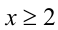
Ответ. 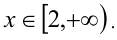
Пример №102.
Решить уравнение { 2х} = x.
Решение:
1-й способ. Заметим, что левая часть уравнения {2х} как величина дробной части может принимать значения, не выходящие за пределы полуинтервала [0,l). Следовательно, и правая часть уравнения, т.е. x, может принимать значения в этих же пределах. Итак, ОДЗ: 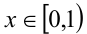 . Разобьём ОДЗ на два промежутка числом 1/2 и на каждом из них раскроем дробную часть и решим уравнение.
. Разобьём ОДЗ на два промежутка числом 1/2 и на каждом из них раскроем дробную часть и решим уравнение.
1) Пусть 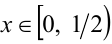 .Тогда
.Тогда 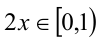 , следовательно,
, следовательно, 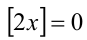 и
и 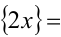
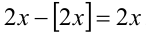 . Поэтому на рассматриваемом промежутке уравнение примет вид
. Поэтому на рассматриваемом промежутке уравнение примет вид 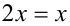 , откуда находим
, откуда находим 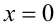 . Поскольку найденное значение принадлежит
. Поскольку найденное значение принадлежит 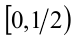 , то, следова-тельно, будет решением.
, то, следова-тельно, будет решением.
2) Пусть теперь 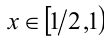 . Тогда
. Тогда 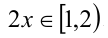 , а значит,
, а значит, 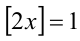 и
и 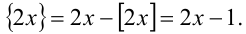 Поэтому на данном промежутке уравнение примет вид
Поэтому на данном промежутке уравнение примет вид 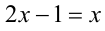 , откуда находим
, откуда находим 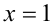 . Однако это значение не принадлежит рассматриваемому полуинтервалу и поэтому не будет решением.
. Однако это значение не принадлежит рассматриваемому полуинтервалу и поэтому не будет решением.
2-й способ (графический). Построим в одной системе координат графики функций 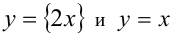 , стоящих в левой и правой частях уравнения. Количество решений уравнения при этом равно количеству точек пересечения этих
, стоящих в левой и правой частях уравнения. Количество решений уравнения при этом равно количеству точек пересечения этих
графиков, а сами решения являются абсциссами точек пересечения графиков. Очевидно, что графики пересекаются в единственной точке — начале координат. Проверкой убеждаемся, что число x = 0 действительно является решением данного уравнения (проверку сделать необходимо, поскольку графический способ решения, вообще говоря, неточный).
Пример №103.
Сколько решений имеет уравнение
x + [100x]=100x?
Решение:
Перепишем уравнение в виде x = {100х} . Эту задачу можно решить графически. Рассмотрим другой способ. Так как выражение {100x} может принимать значения лишь из промежутка [0,1), то и 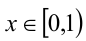 . Но тогда x можно представить в виде бесконечной десятичной дроби
. Но тогда x можно представить в виде бесконечной десятичной дроби
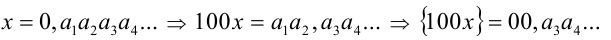
Подставим в исходное уравнение: 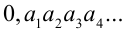
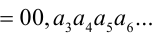
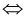
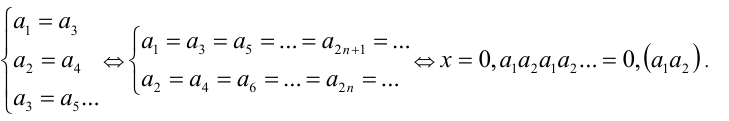
Таким образом, любое число вида 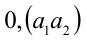 удовлетворяет уравнению. Найдём, сколько всего существует таких чисел. Цифра
удовлетворяет уравнению. Найдём, сколько всего существует таких чисел. Цифра 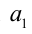 может принимать 10 значений (от 0 до 9), при этом для каждого такого значения вторая цифра
может принимать 10 значений (от 0 до 9), при этом для каждого такого значения вторая цифра 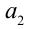 также может принимать 10 значений (от 0 до 9). Всего имеем 10×10 возможностей. Но надо исключить случай x = 0,999… = 1. Ответ: 99 решений.
также может принимать 10 значений (от 0 до 9). Всего имеем 10×10 возможностей. Но надо исключить случай x = 0,999… = 1. Ответ: 99 решений.
Пример №104.
Найти целую часть числа 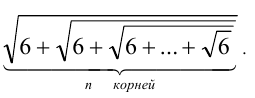
Решение:
Для решения задачи достаточно оценить, между какими последовательными целыми числами расположено данное число. Обозначим это число через 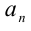 . Оценка снизу находится несложно, поскольку очевидно, что при любом натуральном n имеем
. Оценка снизу находится несложно, поскольку очевидно, что при любом натуральном n имеем 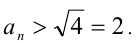 Найдём оценку сверху для
Найдём оценку сверху для 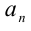 . Для этого заменим в выражении для
. Для этого заменим в выражении для 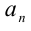 последний радикал
последний радикал 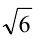 на
на 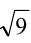 :
:
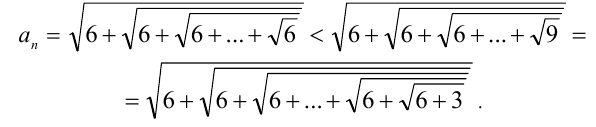
Последовательно упрощая выражение в правой части, получим 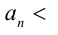
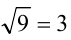 . Итак,
. Итак, 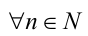 справедливо
справедливо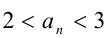 , откуда
, откуда 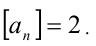
Пример №105.
Решить уравнение 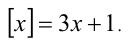
Решение:
Разобьём множество всех действительных значений неизвестной x на промежутки, в которых можно однозначно раскрыть целую часть: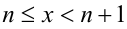 , где
, где 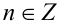 . Решим задачу на каждом из этих промежутков. Так как при
. Решим задачу на каждом из этих промежутков. Так как при 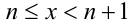 имеем
имеем 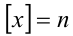 , то подставим в исходное уравнение, и оно примет вид
, то подставим в исходное уравнение, и оно примет вид 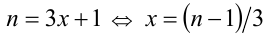 . Учтём, что найденное значение x будет решением уравнения в том и только в том случае, если оно принадлежит рассматриваемому промежутку, т.е.
. Учтём, что найденное значение x будет решением уравнения в том и только в том случае, если оно принадлежит рассматриваемому промежутку, т.е. 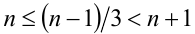 . Решая систему
. Решая систему
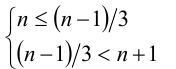
в целых числах, находим 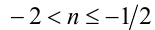 , т.е.
, т.е. 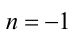 . Тогда
. Тогда 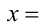
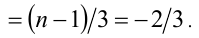
Замечание. Задачу можно было решить, используя графический подход.
Пример №106.
Решить уравнение 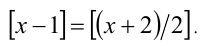
Решение:
Положим 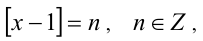 тогда в силу уравнения и
тогда в силу уравнения и 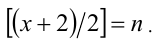 Отсюда имеем
Отсюда имеем
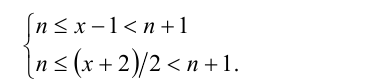
Дальнейшее решение зависит от того, что больше: x —1 или (х + 2)/2. Рассмотрим два случая.
1) Пусть 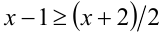 , т.е.
, т.е. 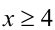 . В этом случае имеем:
. В этом случае имеем:
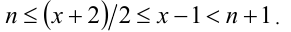
Получаем систему неравенств с двумя неизвестными, одна из которых целочисленна:
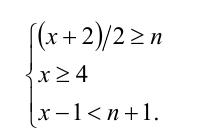
Отсюда 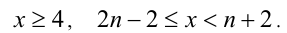 Следовательно,
Следовательно, 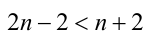
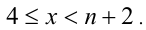 Из неравенств
Из неравенств 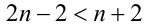 и
и 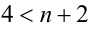 находим, что
находим, что 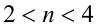 . Последнему неравенству удовлетворяет только одно целое число
. Последнему неравенству удовлетворяет только одно целое число
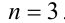 Подставляя в неравенства (1), определяем
Подставляя в неравенства (1), определяем 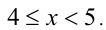
2) Пусть 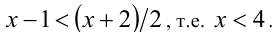 В этом случае получаем
В этом случае получаем
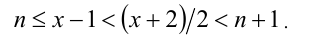
Аналогично первому случаю находим 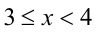 . Объединяя полученные решения, приходим к окончательному ответу.
. Объединяя полученные решения, приходим к окончательному ответу.
Ответ: 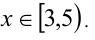 .
.
Пример №107.
Решить уравнение
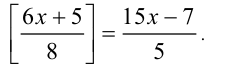
Решение:
Сделаем замену 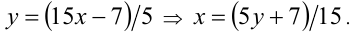 Переходя к новой переменной, получим уравнение
Переходя к новой переменной, получим уравнение
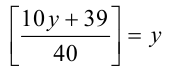
с целочисленной неизвестной у . Раскрывая целую часть по определению, получаем двойное неравенство
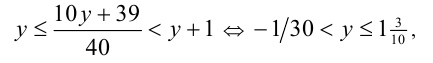
откуда с учётом целочисленности у находим у = 0 или у = 1. Им отвечают значения x = 7/15 и x = 4/5.
Ответ: 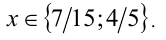
Пример №108.
Найти все решения уравнения 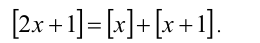
Решение:
Упростим уравнение при помощи свойств целой части. Так как 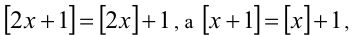 то уравнение принимает вид
то уравнение принимает вид
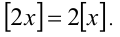
Решим его стандартным методом. Чтобы раскрыть обе целые части, разобьём множество всех действительных x на полуинтервалы 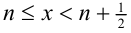 и
и 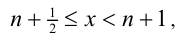 где
где 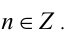
1) Если 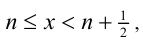 то
то 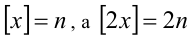 (так как
(так как 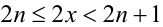 , и уравнение на этом промежутке принимает вид
, и уравнение на этом промежутке принимает вид 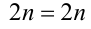 — верно при любом
— верно при любом 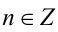 , т.е. при любом целом n любое
, т.е. при любом целом n любое 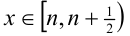 удовлетворяет уравнению.
удовлетворяет уравнению.
2) Если же 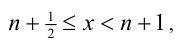 то
то 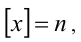 а
а 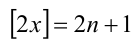 (так как
(так как 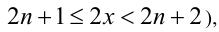 и тогда уравнение примет вид
и тогда уравнение примет вид 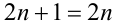 неверно ни при каком
неверно ни при каком 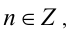 , т.е. ни одно значение x из рассматриваемого промежутка не удовлетворяет уравнению.
, т.е. ни одно значение x из рассматриваемого промежутка не удовлетворяет уравнению.
Ответ: 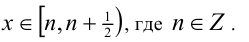
Пример №109.
Найти все решения уравнения {х} = 1/х.
Решение:
ОДЗ: 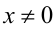 . Перепишем уравнение в виде
. Перепишем уравнение в виде
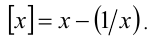
Пусть 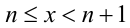 , где
, где 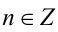 . Тогда
. Тогда 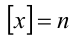 , и уравнение на указанном промежутке примет вид
, и уравнение на указанном промежутке примет вид
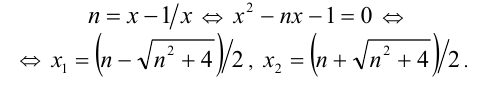
При этом 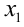 , не удовлетворяет условию
, не удовлетворяет условию 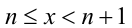 ни при каком
ни при каком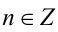 , а
, а 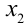 , удовлетворяет ему при
, удовлетворяет ему при 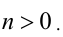
Ответ: 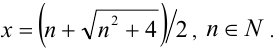
Пример №110.
Найти все натуральные значения n, удовлетворяющие уравнению
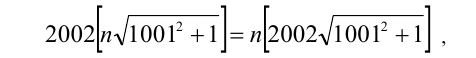
где [х] — наибольшее целое число, не превосходящее числа x.
Решение:
Пусть 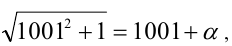 тогда
тогда
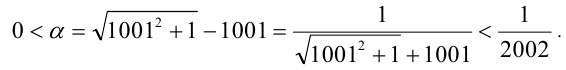
Значит, 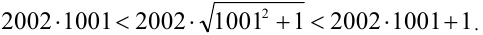
Но тогда 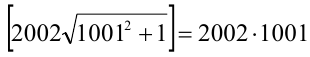 , поэтому, в силу уравнения,
, поэтому, в силу уравнения,
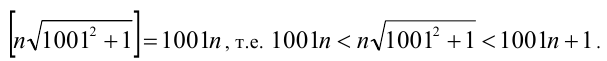
Отсюда 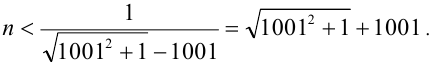
Ответ: 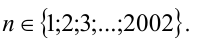
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

