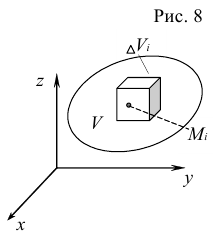
Пусть в замкнутой области 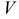 в декартовой системе координат
в декартовой системе координат 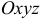 задана непрерывная функция
задана непрерывная функция 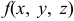 . Разобьем область
. Разобьем область 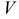 на
на 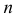 ячеек
ячеек 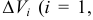
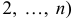 и возьмем точки
и возьмем точки 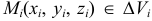 (рис. 8). Составим сумму
(рис. 8). Составим сумму 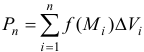 . Эта сумма называется интегральной суммой для функции
. Эта сумма называется интегральной суммой для функции 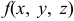 в области
в области 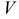 .
.
Тройным интегралом 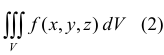 от функции
от функции 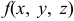 , распространенным на область
, распространенным на область 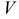 , называется предел интегральной суммы
, называется предел интегральной суммы 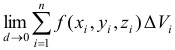 при
при 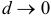 , если этот предел существует и не зависит от формы ячеек
, если этот предел существует и не зависит от формы ячеек 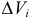 , и выбора точек
, и выбора точек 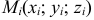 в них, где
в них, где 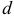 — наибольший диаметр ячеек
— наибольший диаметр ячеек 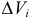 . В прямоугольных координатах элемент объема
. В прямоугольных координатах элемент объема 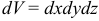 .
.
Свойства тройного интеграла аналогичны свойствам двойного интеграла.
Вычисление тройного интеграла сводится к вычислению трехкратного интеграла
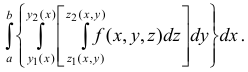
В результате интегрирования по 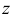 и подстановки пределов в фигурных скобках получится функция от
и подстановки пределов в фигурных скобках получится функция от 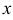 и
и 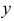 . Далее вычисляется двойной интеграл от этой функции.
. Далее вычисляется двойной интеграл от этой функции.
Масса 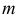 тела, занимающего область
тела, занимающего область 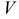 , с объемной плотностью
, с объемной плотностью 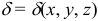 , статические моменты
, статические моменты 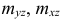 и
и 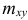 , координаты центра тяжести
, координаты центра тяжести 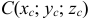 моменты инерции относительно осей
моменты инерции относительно осей 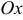 ,
, 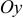 и
и 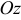 (
(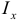 ,
, 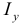 и
и 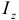 ) и начала координат
) и начала координат 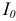 выражаются по формулам:
выражаются по формулам:
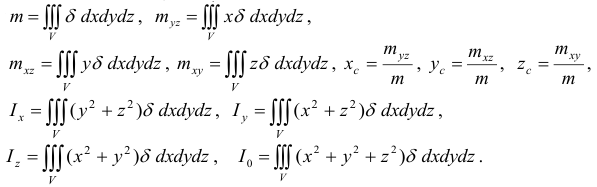
Переход тройного интеграла в прямоугольных координатах в тройной интеграл в цилиндрических координатах осуществляется по формулам: 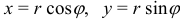 ,
, 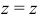 ; элемент объема
; элемент объема 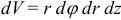 . При этом уравнения поверхностей, ограничивающих область интегрирования, также преобразуются к цилиндрическим координатам:
. При этом уравнения поверхностей, ограничивающих область интегрирования, также преобразуются к цилиндрическим координатам:
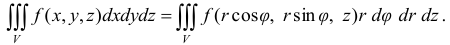
Переход тройного интеграла в прямоугольных координатах в тройной интеграл в сферических координатах осуществляется по формулам: 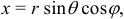
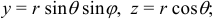 элемент объема
элемент объема 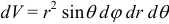 . При этом уравнения поверхностей, ограничивающих область интегрирования, также преобразуются к сферическим координатам:
. При этом уравнения поверхностей, ограничивающих область интегрирования, также преобразуются к сферическим координатам:
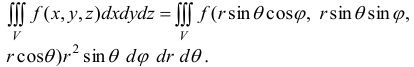
Пример:
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: 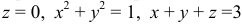 . Сделать чертежи данного тела и его проекции на плоскость
. Сделать чертежи данного тела и его проекции на плоскость 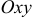 .
.
Решение:
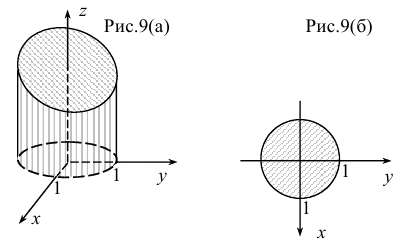
Тело, ограниченное плоскостями 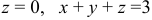 и цилиндром
и цилиндром 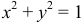 , изображено на рис. 9(a). Его проекция на плоскость
, изображено на рис. 9(a). Его проекция на плоскость 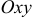 является кругом с радиусом
является кругом с радиусом 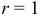 (рис. 9(б)). Объем тела равен
(рис. 9(б)). Объем тела равен
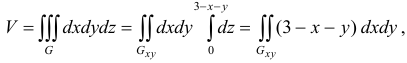
где 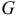 — область, занимаемая данным телом;
— область, занимаемая данным телом; 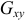 — ее проекция на плоскость
— ее проекция на плоскость 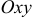 . Линия, ограничивающая плоскую область
. Линия, ограничивающая плоскую область 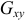 , есть окружность
, есть окружность 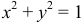 . Переходя к полярным координатам
. Переходя к полярным координатам 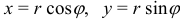 ,
, 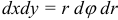 , найдем:
, найдем:
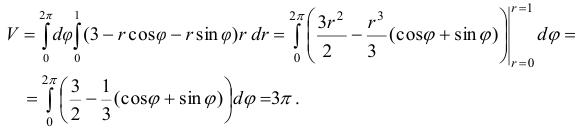
Ответ. 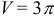 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Метод наименьших квадратов |
| Двойной интеграл |
| Криволинейный интеграл |
| Векторный анализ: основные понятия и пример с решением |

