Оглавление:









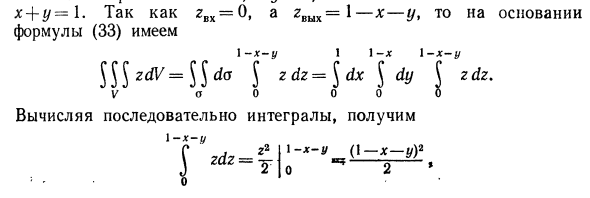






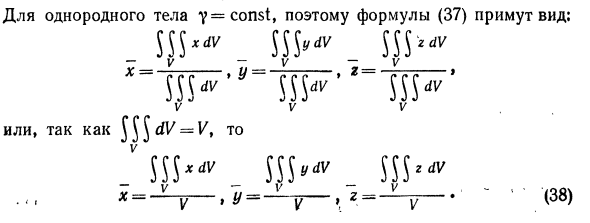


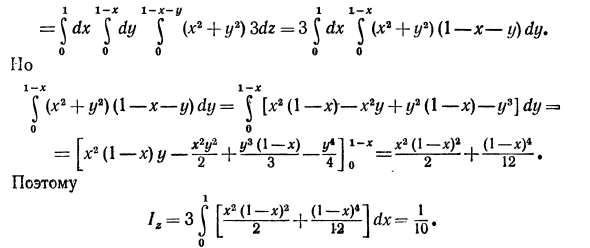
Тройной интеграл
- Тройной интеграл /. Массовая проблема Для данного объекта V в пространстве Оуга рассмотрим небольшой объект AK, содержащий часть, то есть точку P (x \ y \ r). Отношение массы Am этого небольшого тела к его объему AV, Другими словами, это называется средней плотностью тела AV. Если это существует о Реляционный предел лимита — когда тело AV сокращается До точки P (x \ y \ r) этот предел называется плотностью в точке P. Поскольку это зависит от положения точки P (x \ y \ r), она является функцией ее координат: y-y (x, y, r) вычисляет массу / h тела объема V. Известно, что плотность каждой точки на теле является непрерывной функцией координат точки P (x \ y; r). у = у (х, у, г).
Вычислить двойной интеграл по площади функции L (x, y) I / (* «* /» d) Декартовы координаты dz (см. § 1, пункт 4, формула (I)), я <. у) Мы получаем (H (x, y) \ bφ2 (x) / h (x, y)} W 5 f (xty, z) dz \ do = \ dx ] J f (xty, z) dz \ dy. o ‘g (x, y)) aφ, (x) \ g (X, y) J Вот так (32) bΦ, () / h (x.y) \ SJJ / (* f.Z) dV = \ dx \ $ f (xty, z) dz \ dy. V aφ, (X) \ g (X.y))
Получите тройное интегральное значение, проецируя область V на плоскость Oxu. Людмила Фирмаль
Если вы опустите фигурные скобки, выражения (31) и (32) обычно записываются в следующем формате: ч (х, у) \\ f (x, ytz) dV = ^ do \ f (x, y, z) dz или ‘° 5 (33) Ish f, (x) h (x.y) x [\ f (x, ytz) dV = \ dx \ dy \ f (x, y, z) dz. V aφ, (X) g (x, y) Если область V является более сложной, чем рассматриваемая область, она делится на конечное число областей Vlt V2, и тип Vk и показанное уравнение (33) применяются к каждой из них. Благодаря аддитивности интеграл всей области равен сумме интегралов каждой области I7, -.
Пример. Рассчитать тройной интеграл JSS2 ^ v Интеграл V представляет собой пирамиду, окруженную плоскостью a: -0, y = 0, z = 0, x + y + r = 1 (рис. 249). Решения. Площадка А, где проецируется пирамида, представляет собой неплоскостной треугольник. Прямая линия х = 0, у = 0, х + у = 1 zBX = 0 и zBblx = l — x — y, поэтому, используя уравнение (33), 1 х 1 1 х 1 $ r <b = \ ax 5 dy J zdz. О, оооо Если интеграл рассчитывается непрерывно,
| Скалярное поле | Числовые ряды |
| Экстремум функций двух переменных | Функциональные ряды |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
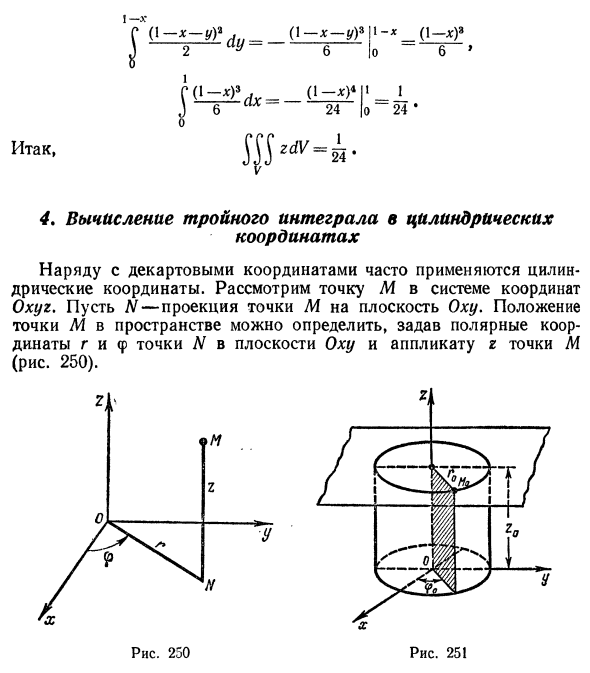
- 1 х (1-x-yy _ (1-x-y) «[1-x_ (1- *)» o U A L A » (Lzf)? Z / y.- (L = £ 14 6 «24 Я Я _ [ O 24 * так 4. Расчет цилиндрического тройного интеграла координировать Наряду с декартовыми координатами часто используются цилиндрические координаты. Рассмотрим точку M в системе координат Оку, и пусть N — проекция точки M на плоскость Окси. Положение точки M в пространстве можно определить, установив полярные координаты r и f точки N в плоскости Oxy и перекрывая z точки M (рисунок 250). 1 24 ‘
Цилиндрические координаты точки связаны с декартовыми координатами x, y, z следующим соотношением: x-g COS f, y = r sinq), 2 = 2 (34) Точка M0 с координатами в декартовой системе координат (X0 \ y0; 20) — пересечение плоскости x = x0 и y-y0. z 2p. В цилиндрической системе координат точка M0 (r0 \ <p0; 20- Является ли пересечение трех поверхностей: r = r0, φ = φ0, z = 20 (рис. 251).
Эти три числа r, cp и z называются цилиндрическими координатами точки М. Людмила Фирмаль
Первое уравнение r = r0 явно соответствует прямому цилиндру радиуса r0 в пространстве, а его генератор параллелен оси Og (ось цилиндра). Отметим, что если r0 = 0, цилиндр выродится в ось Og. Уравнение φ = φ0 соответствует полуплоскости, которая проходит через ось Og и составляет угол φ0 с плоскостью Ox. Уравнение r-r0 соответствует плоскости, параллельной плоскости Oxu, и где r0 пересекает ось Og в одной точке.
Таким образом, существует три семейства поверхностей, называемых координатными поверхностями: r = const, φ = const, 2 = const. Уравнение r = * / (x, y) пространственно соответствует грани. Подставляя представление для цилиндрических координат с использованием уравнения (34) вместо x, y, r, получают поверхностное уравнение с цилиндрическими координатами z-f (r cosφ, r sinφ). При переходе от декартовых координат к цилиндру вычисление тройного интеграла часто значительно упрощается. Предположим, вам нужно вычислить тройной интеграл J $ / (x, y> r) dV v Над областью V Оугского пространства.
Как известно, справедливо следующее уравнение (33). l <, у) SS $ / (. Sf (x, y9z) dz, v o g (x, y) Где o — область плоскости Oxy, которая является проекцией тела V, а g (x, y) и h (x, y) — претенденты на вход и выход. Предположим, что область o является двойным интегралом на рисунке 252 Этот регион легче рассчитать в полярных координатах. Тогда выражение (33) можно записать в следующем формате: h (g cos f. g sin f) $$$ / (*. Y> z) d.V = da 5 / (r cos y, r sin <p, z) dz. V a g (g cos f, g sin f) Применяя правила для вычисления полярных двойных интегралов и вычисления двойного интеграла в правой части последнего уравнения:
В полярных координатах 3 g, (f) h (g cos f, g sin f) l \ lf (x9y, z) dV = \ dph ^ rdr $ / (govsf, rsin <p ;; e) <&, (33 ‘) V a Mf) & {gcosy, g 81pf) Где MF) = GVX, / • «(φ) = / * out- Это формула для вычисления тройного интеграла цилиндрических координат. Пример. Если плотность y любой точки равна расстоянию r от этой точки до оси цилиндра, определите массу m прямого цилиндра V с высотой H и радиусом Rt. у = Решения. Выберите систему координат, как показано. 252.
Масса m цилиндра V равна тройному интегралу плотности y: V v Где область интеграции — цилиндр V. Вычислить этот интеграл в цилиндрических координатах. Проекция цилиндра на плоскость Оху представляет собой круг с радиусом R с центром в начале координат. Применяя формулу (33 ‘): 2nd R N 2nd R m = J dy ^ rdr ^ rdz = H \ dy = V LLC 00 Итак, желаемая масса 2л Я3 //
Тройная интеграция приложения Принципы, лежащие в основе применения тройных интегралов к решению физических задач, аналогичны принципам, лежащим в основе применения двойных интегралов, описанных в § 6 § 1. Рассмотрим некоторые из этих задач. Статический момент центр тяжести. Известно, что статический момент Sxy точки массы m относительно плоскости Ohu является произведением точечной массы и ее копии: Sxy = mz. Статические моменты Syz и Sxz определяются аналогично в отношении плоскостей Og и Oxz: Syz = mx} Sxz = my.
Если указана система, состоящая из нескольких точек массы, ее статический момент определяется как сумма соответствующих статических моментов точек массы, составляющих эту систему. Предположим, что объект V задан в пространстве, а его плотность является функцией координат этой точки в любой точке: y = y (x, y, r). Рассчитайте статический момент Sxy этого объекта. Разделите тело V на n маленьких тел ДУ, — (i = 1, 2, …, n).
Для каждого малого тела DK выберите произвольно в точке Pt (xt; y {\ z {). Предполагая приблизительно плотность каждой точки тела ДУ, которая является константой, равной плотности выбранной точки Ph, мы можем получить приближенное выражение для массы Дт этого тела. Am, y (xh y {, z {) bVt. Замените все мелкие объекты DV массой P, (x, u9, y, r) и массой Dm {. Статический момент этой точки относительно
Плоскость династии Оху дает приближение статического момента DS’xy. ДУХ «2, Dt», z, y (xit yit Zj) AV, Из-за аддитивности статический момент всего объекта равен сумме статических моментов объекта .. ДУ4 .. Следовательно, в случае Sxy получается следующее приближенное уравнение. N S Да 2 , -Y (, -. UitZg) я— 1 В ограничении, если маленький объект AV-t уменьшен до точки, вы получите точное значение статического момента. Sxy = lim J] 2, -y (xh yit z () bVt = mzy (x, yf z) dV. n- + »J = 1 В так Sxy = \ [\ zy (x, y, z) dV. (35): v Аналогично, для статического момента объекта V относительно плоскостей Ойза и Ог, = \ А z) dV> s ** = IS 5 * 1 (x * y> z) dV • (35,) V v ■
Координаты x, y, z центра тяжести тела V определяются тем же уравнением, что и уравнение (23), раздел 6, § 1:. ‘; (36) Где m — масса тела V. Масса m тела V в этом разделе равна «р». Согласно 2, формула m =? (* »Y * 2) Потому что это определяется по dV Затем, применяя уравнения (35 ‘), (35) и (36), вы можете видеть, что: JJJ * v (*. Y. *) DV HW (Jtt y’z) dV J J J v. от x до iHv (jr’y’z) dv9y themv (jrt y’z) dv’z ^ ‘(37)
В случае однородного y = const, поэтому выражение (37) имеет следующий вид: tyxdV _ AI _ V v V Или с тех пор = Если V равномерно, то есть плотность y в каждой точке, то Ge одинакова и равна y0, а его масса m равна m = y0V9 (30) Где V — объем тела В общем случае плотность (y) изменяется от точки к точке, поэтому уравнение (30) не подходит для определения веса.
Поэтому действуйте следующим образом: Разделите тело V на n маленьких тел AV \, …, AV N Y = 2 LU /. Для каждого маленького AV выберите с точкой P (xy, z). j = я Если взять объект достаточно малым, плотность в каждом таком объекте будет немного меняться и не сильно отличается от плотности y {-y (P,) = y (xit yit Zj) в точке P , Учитывая плотность в каждой точке малого тела AV, она является постоянной величиной и равна плотности в точке P — приблизительно вычислена масса Am. Am, y y, AVj = y (*, -. Un *,) (t = 1, 2 ….. n). N Масса всего тела м 2, / -1 Числа почти равны: н н m = 2 A «* /» 2 Y (* /. Y <> * /) я = I / = P
Для точного значения массы m мы берем этот предел интегральной суммы, когда каждое из тел AV сжимается в точку. N m = lim 2 Y (* / »Y, -, A K, -. p- »oo /« 1 Решение проблемы веса состояло в том, чтобы рассмотреть определенный тип общего предела. Многие проблемы, такие как геометрия, физика и т. Д., Смягчаются путем нахождения такого общего предела, поэтому независимо от этой проблемы или проблемы, изучите характеристики таких общих пределов в общем виде. Делать это естественно и приводит к понятию тройного интеграла.
Пример. Найдите центр тяжести однородного тела, окруженного параболоидом 2z = 4-x% -y% и плоскостью r = 0 (рис. 253). Решения. Основываясь на симметрии тела относительно координатных плоскостей Ohu и Og, мы заключаем, что центроид находится на оси Og и, следовательно, x-y-0. Найти перекрытие r центра тяжести, определяемое уравнением (38). г / д / \ Иллинойс 1 неделя Рассчитать объем тела V = JJJdV в Статический момент Sxy = J J J zdV. Рассчитать с US 253 Линдрические координаты: GVH = 0, 4_x2_and1 4_g * j-, hout = -2— = 2 ‘Платформа в самолете ° Оху — круг Поскольку радиус r = 2 вокруг начала координат 4 г * 4-G * 2 V o o o a 2 года 2 8 = 4 4-G » 2 2 л J Mr ^ -iM’4- ^ * -4 «- V O O OO Вот так 8 -GM 8 — Санкт-
Момент инерции. Момент инерции / x точки массы массы m относительно оси Ox равен произведению массы этой точки на квадрат расстояния от этой точки до оси Ox. Поскольку квадрат расстояния точки P (x \ y \ r) до оси Ox равен y2 + z2, 1X = (! / * + R *) т. Момент инерции относительно осей Oy и Og определяется аналогичным образом. /, = (** + r2) t, 12 = (x * + y *) t. Предположим, что V дает тело, плотность которого в любой точке имеет определенную координатную функцию этой точки, то есть y = y (x, y, r).
Найти момент инерции этого объекта относительно координатных осей. Если вы выберете небольшое тело AVif, вы почти сможете увидеть его момент инерции Д11х относительно оси Ox. д /; + Z? ) Y (Xit yir 2 ,.) Д1Л. Приближенный момент инерции тела с использованием аддитивных характеристик момента инерции Vi N K2 (Y * + r?) Y (* /> Yn * /) AVt. я = я В пределе, если каждый маленький объект DC сжимается до некоторой точки, вы получаете точное значение момента инерции. 1x = Pm2 (y1 + r1) y (X; ylf zt) AVt = J J $ + r «) y (*, y, z) dV. С» — / G » так + (39) v Эту же формулу можно получить для момента инерции! Y и + U. = + U. «M ^ (39 ‘) v v Пример. Определите момент инерции вокруг оси O однородной пирамиды V (см. Рис. 249) с плотностью y = 3, окруженной плотностью x = 0, y-0, r-0, x + y + z = 1. Применяя уравнение (39 ‘) y * z) dV = «Jd / jV J V + r,») 3dz = 3 J dx + y2) (1-x-y) dy. ООО 00 эй l] (x * + y *) (\ -x-y) dy = f [x * (\ -xy-x * y + if (\ -x) -y>] dy 0 D 2 / t 4 x2y2. 0s 0-x) X2 (1-xY, (1-x) 4 так
Тройной интеграл и его свойства Дает пространство в пространство, объем которого V. Определите функцию u = f (P) = f (x, y, r) в каждой точке P в этой области. Выполните следующие шаги: 1. Разделите тело на n маленьких тел ДУ, ДУ2. далее Выберите произвольную точку Pi (x (\ y {\ r,) на каждом небольшом объекте DC. Умножьте значение функции u = f (P) на точку P (точка Pfi принадлежит Объем малого объекта AVt flPJAV ^ HX;, yi9 Zj) AVg. 3. Составьте сумму всех таких работ. 2 f (H, -) AV (= i f (* «y» tl) AVt. Эта сумма называется интегральной «суммой». 4.
Рассмотрим предел интегральной суммы с неограниченным увеличением числа n тел AV (и если каждое тело AV сжимается до некоторой точки. Это ограничение существует и делит область V на тело AVlt Если он не зависит от метода или выбора соответствующих им точек Pj (x {\ y; \ r,), его называют тройным интегралом функции u = f (P) r = xf (xt yt z) в области Y Представляется как: lHf (P) dV или ^ f (xty, z) dv. V v Вот так lllHP) dV-f (x, y, z) dV = \ im ± f (x „y, -, r, …) v v Возвращаясь к пункту 1, можно сделать вывод, что масса m объекта V равна тройному интегралу переменной плотности y = y (x, y, r). Y> *) DV-
Вы можете видеть, что тройная интеграция является прямым обобщением двойной интеграции, когда область интеграции является трехмерным объектом. Как и в случае двойных интегралов, существует теорема о существовании тройных интегралов. Теорема существования. Функция u- / (*, y, r), продолжающаяся в ограниченной замкнутой области объема V, имеет тройной интеграл. Другими словами, каждый из них обращен в одну точку.
Это ограничение может быть наложено путем деления области V на части, Тройной интеграл имеет те же характеристики, что и двойной интеграл. 1. Коэффициент постоянной можно извлечь из тройного интегрального символа. Это значит Общий тройной интеграл нескольких функций равен сумме тройных интегралов слагаемых, т. Е. $$$ [/ (*, A r) + y (x, y, Y, *) LF-y, r) * /. v v v 3. Область интеграции f (x, (/, z)> 0 В ■ v 4. Если область интегрирования f (xt y, r) ) dV = f ( o. 1 / o. ^ O) 17, v Где К это регион 6. Свойство аддитивности. Если домен интеграции V делится на k частей Klf … v v, v, y * z) dV • В заключение этого раздела отметим, что если подынтегральное выражение y (z) = l в области V, тройной интеграл численно равен объему области.
Это f (x, y, r) s = в этом случае? 1, то есть N Форма интегральной суммы 2 л, численно равная / = 1 Его тело. 3. Расчет декартового тройного интеграла координировать Вычисление тронного интеграла сводится к последовательному вычислению трех определенных интегралов. Предположим, что область интегрирования V является объектом, который находится внизу на поверхности z = g (x, y) и вверх на поверхности r = h (x, y). Спроецируйте это тело на плоскость Oxu области a, окруженной кривой V = ()> V = φα () [<Pi (x) ^ φ2 (*)] и прямой линией.
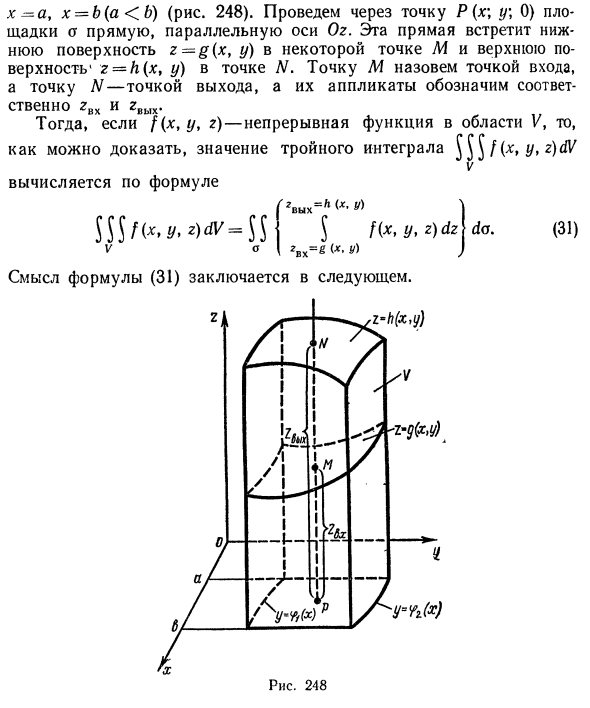
х-а, х = b (а <b) (фиг. 248). Нарисуйте прямую линию, параллельную оси Oz, которая проходит через точку P (x \ y \ 0) в области a. Эта прямая линия встречает нижнюю поверхность z = g (x, y) в некоторой точке M и верхнюю поверхность r = A (x, y) в N. Точка M называется точкой входа, точка N становится точкой выхода, и отображается заявитель. По словам Собственно ГВХ и 2ВЫх. Тогда, если f (x, y, z) является непрерывной функцией области V, Значение тройного интеграла J ^ / (x, y, z) dV, чтобы мы могли доказать v Рассчитать по формуле • out = l (x. Y) \ f (x, y, z) dz Вы. (31) V a Значение уравнения (31) следующее: Рис. 248 х
Чтобы вычислить тройной интеграл J ^ f (x, y, z) dV, h (X.y) Сначала нам нужно вычислить конкретный интеграл J f (x, y} z) dz. К (Х. у) Предположим, что x и y постоянны. Нижним пределом интеграции является приложение в точке входа M: zBX-g (x, y), а верхней границей интеграции является приложение zBHX = f (x, y) в конечной точке приложения N. Результатом этого интегрирования является функция двух переменных x и y. Когда эта функция интегрирована в область а,

