Тригонометрия
Начнем с определений:
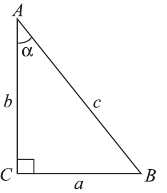
1.В прямоугольном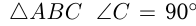 
, 
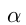— острый угол 
, 
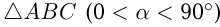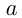и 
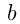— катеты, 
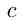— гипотенуза. Синусом угла 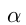называется отношение противолежащего катета 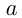к гипотенузе 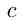; косинусом угла 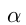называется отношение прилежащего катета 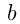к гипотенузе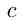; тангенсом угла 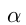называется отношение противолежащего катета к прилежащему; котангенсом угла 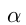называется отношение прилежащего катета к противолежащему:
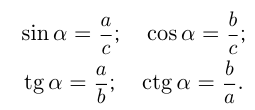
Углы здесь и в дальнейшем измеряются в градусах либо в радианах.
Один градус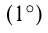 
— это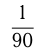 
величины прямого угла, или 
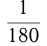величины развернутого угла. Один радиан (1 рад) — центральный угол, длина дуги которого равна радиусу. 1 рад =
; 
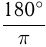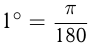рад; 1 рад 
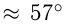. Полный угол равен 360°или 
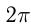рад. Развернутый — 180° или 
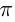рад.
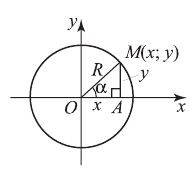
2.Рассмотрим единичную окружность в прямоугольной системе координат с центром в начале координат и радиусом, равным 1. Возьмем на этой окружности произвольную точку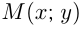 
, соединим ее с началом координат и отметим ее ординату и абсциссу.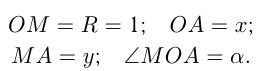
Получим прямоугольный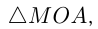 
ордината 
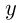— катет, противолежащий углу 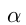, абсцисса 
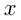— катет, прилежащий к углу .
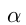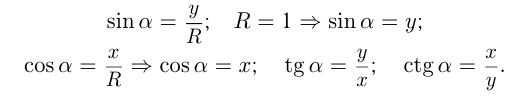
Каждой точке на окружности соответствует единственный угол, образуемый радиусом, проведенным в эту точку, с осью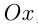 
, и обратно, каждому углу между 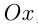и радиусом соответствует единственная точка на окружности, а, следовательно, единственное значение синуса, косинуса, тангенса и котангенса.
При движении точки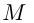 
против часовой стрелки образуются положительные углы, по часовой стрелке — отрицательные. Началом отсчета считается точка с координатами 
.
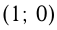Сделав полный оборот, радиус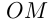 
образует полный угол. Точка 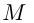, двигаясь дальше по окружности, образует углы, принимающие сколь угодно большие значения. Таким образом, аргумент 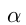в функциях 
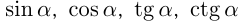: может принимать любое числовое значение. Функции 
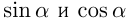повторяют свои значения с периодом 
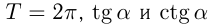— с периодом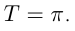 
Знаки 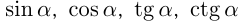зависят от той четверти, в которой находится угол .
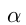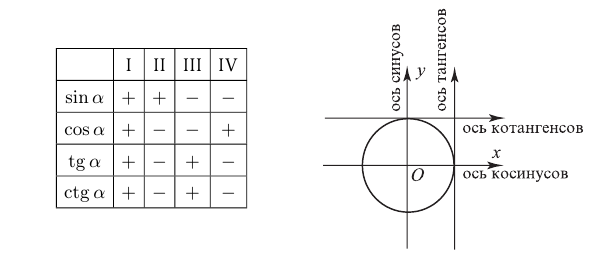
Ось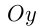 
называется осью синусов, ось 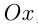— осью косинусов. Оси тангенсов и котангенсов показаны на рисунке.
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Вычислить значение выражения задачи с решением |
| Доказать рациональность числа задачи с решением |
| Основные тригонометрические формулы |
| Вычисление значений тригонометрических выражений задачи с решением |
