Часто при изучении функций появляется необходимость представления данной функции при помощи других функций, которые называют базовыми и свойства которых считаются известными. Пусть дана система базовых функций 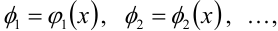
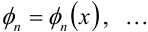 Представить данную функцию
Представить данную функцию  при помощи заданных базовых функций означает разложить функцию
при помощи заданных базовых функций означает разложить функцию  в функциональный ряд
в функциональный ряд 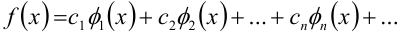 , где коэффициенты
, где коэффициенты 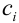 — действительные числа. Имея такое представление, можно аппроксимировать данную функцию при помощи частичных сумм соответствующего функционального ряда.
— действительные числа. Имея такое представление, можно аппроксимировать данную функцию при помощи частичных сумм соответствующего функционального ряда.
Во многих технических задачах возникает необходимость представлять произвольные функции через простейшие периодические функции. Такие задачи часто возникают в электротехнике, радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования. Например, в электротехнике требуется представить ток, изменяющийся по сложному закону 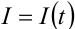 , через простые синусоидальные токи
, через простые синусоидальные токи 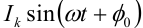 . Математическим аппаратом для исследования таких задач служат ряды, для которых тригонометрические функции взяты в качестве базовых.
. Математическим аппаратом для исследования таких задач служат ряды, для которых тригонометрические функции взяты в качестве базовых.
Тригонометрическим рядом называется функциональный ряд вида
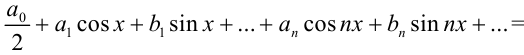
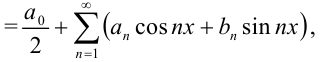
где действительные числа 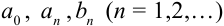 — коэффициенты ряда.
— коэффициенты ряда.
Пусть  — произвольная периодическая функция с периодом
— произвольная периодическая функция с периодом 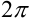 . Допустим, что
. Допустим, что  представляется тригонометрическим рядом:
представляется тригонометрическим рядом: 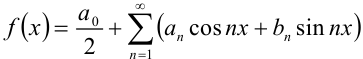 . Так как
. Так как  имеет период
имеет период 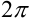 , то её можно рассматривать в любом промежутке длины
, то её можно рассматривать в любом промежутке длины 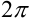 . В качестве основного промежутка возьмём отрезок
. В качестве основного промежутка возьмём отрезок 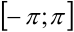 . Предположим, что тригонометрический ряд функции
. Предположим, что тригонометрический ряд функции  сходится на
сходится на 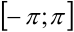 , следовательно, его можно почленно интегрировать (свойство 4 лекции 35). Вычислим коэффициенты
, следовательно, его можно почленно интегрировать (свойство 4 лекции 35). Вычислим коэффициенты 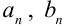 ряда. Для этого проинтегрируем в пределах от
ряда. Для этого проинтегрируем в пределах от 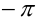 до
до 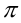 обе части равенства
обе части равенства
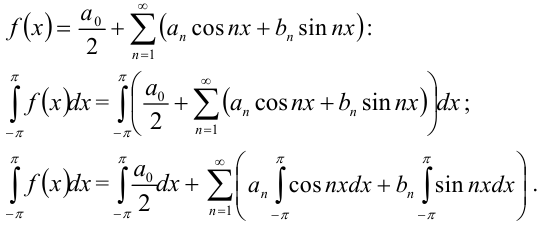
Поскольку 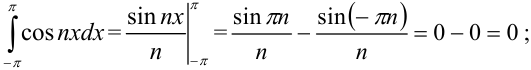
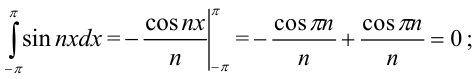
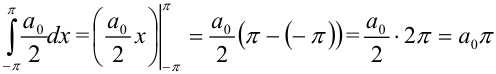 , получим
, получим 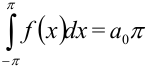 .
.
Отсюда 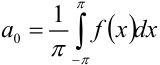 .
.
Умножим обе части равенства 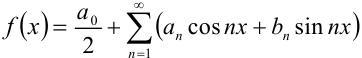 на
на 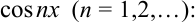
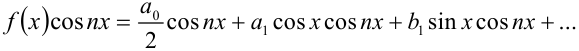 . Почленно проинтегрируем полученное равенство в пределах от
. Почленно проинтегрируем полученное равенство в пределах от 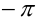 до
до 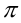 :
:
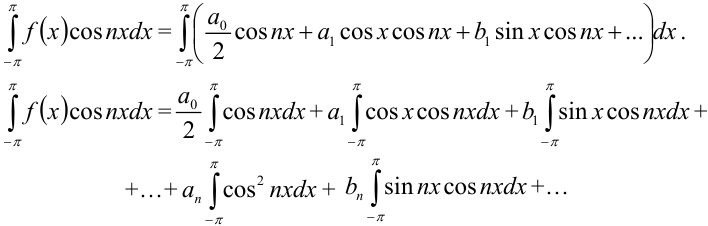
Нетрудно, непосредственно вычисляя определённые интегралы, убедиться в том, что все члены ряда из правой части этого равенства равны нулю, кроме члена 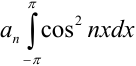 . Значит,
. Значит, 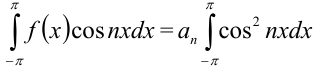 . Вычислим отдельно определённый интеграл
. Вычислим отдельно определённый интеграл 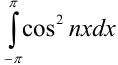 :
:
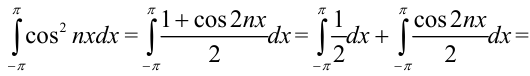
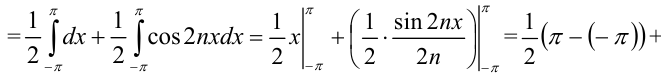
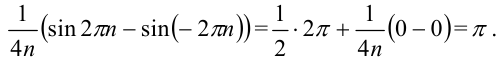
Таким образом, получим 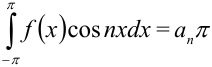 .
.
Отсюда 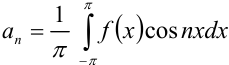 , где
, где 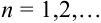
Аналогично, умножив обе части равенства 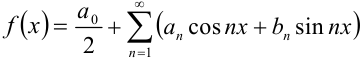 на
на 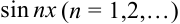 и проинтегрировав его почленно на отрезке
и проинтегрировав его почленно на отрезке 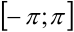 , получим:
, получим:
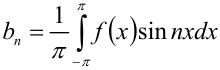 , где
, где 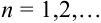
Числа 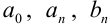 , определяемые формулами
, определяемые формулами 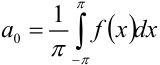 ,
, 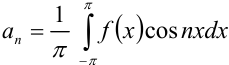 ,
, 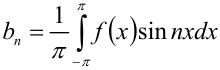 называются коэффициентами Фурье для функции
называются коэффициентами Фурье для функции  .
.
Тригонометрический ряд 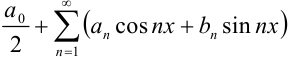 , коэффициенты которого совпадают с коэффициентами Фурье для функции
, коэффициенты которого совпадают с коэффициентами Фурье для функции  , называется рядом Фурье для функции
, называется рядом Фурье для функции  .
.
Таким образом, каждой интегрируемой на отрезке 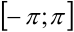 функции
функции  можно сопоставить её ряд Фурье. При этом функция
можно сопоставить её ряд Фурье. При этом функция  называется порождающей функцией для своего ряда Фурье.
называется порождающей функцией для своего ряда Фурье.
Пример №37.1.
Составьте ряд Фурье для функции 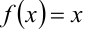 на отрезке
на отрезке 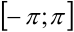 .
.
Решение:
Ряд Фурье для функции  имеет вид
имеет вид 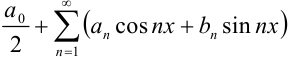 , где
, где 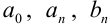 — коэффициенты Фурье. Составим его для функции
— коэффициенты Фурье. Составим его для функции 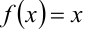 , вычислив коэффициенты Фурье по соответствующим формулам.
, вычислив коэффициенты Фурье по соответствующим формулам.
Найдем 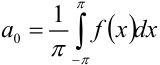 . В нашем случае
. В нашем случае
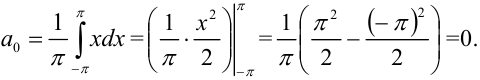
Таким образом, 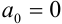 .
.
Найдём 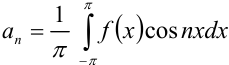 . В нашем случае
. В нашем случае 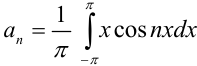 . Вычислим отдельно определённый интеграл
. Вычислим отдельно определённый интеграл 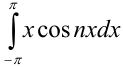 методом интегрирования по частям:
методом интегрирования по частям:
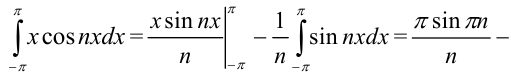
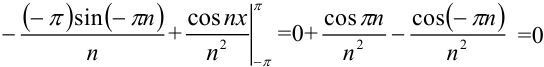
Таким образом, 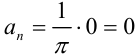 .
.
Найдём 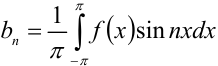 . В нашем случае
. В нашем случае 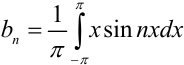 . Вычислим отдельно определённый интеграл
. Вычислим отдельно определённый интеграл 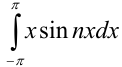 методом интегрирования по частям:
методом интегрирования по частям:
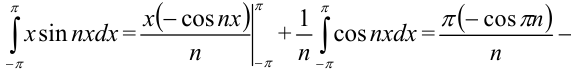
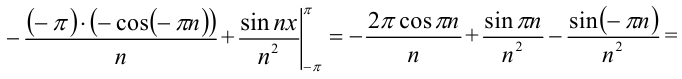
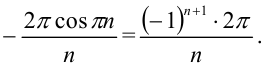
Таким образом, 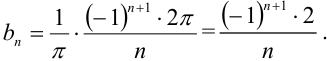
Следовательно, функции 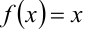 соответствует ряд Фурье
соответствует ряд Фурье
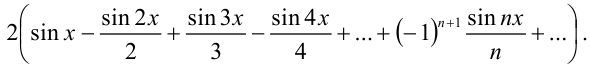
Ответ: функции 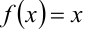 соответствует ряд Фурье
соответствует ряд Фурье
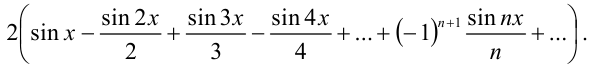
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Практическое применение разложений функций в ряд. |
| Тригонометрический ряд Фурье. |
| Разложение в ряд Фурье чётных и нечётных функций, функций произвольного периода. |
| Понятие дифференциального уравнения. |

