Тригонометрический ряд Фурье
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.
Тригонометрическим рядом называется функциональный ряд вида
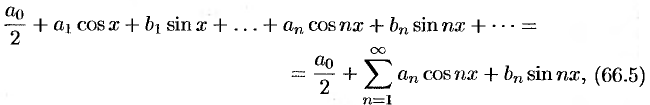
где действительные числа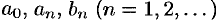 
называются коэффициентами ряда.
Ряд (66.5) можно записать в виде
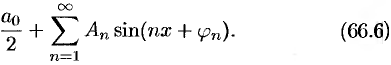
Действительно, положив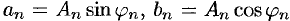 
, получим 
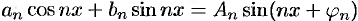; ряд (66.5) принимает вид (66.6) при этом 
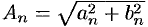и 
.
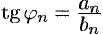Свободный член ряда записан в виде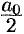 
для единообразия получающихся в дальнейшем формул.
Приведем формулы, которые понадобятся нам в дальнейшем.
Считая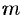 
и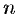 
целыми положительными, находим:
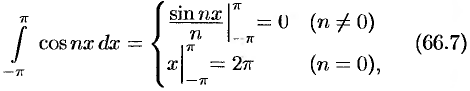
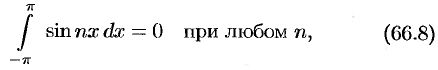
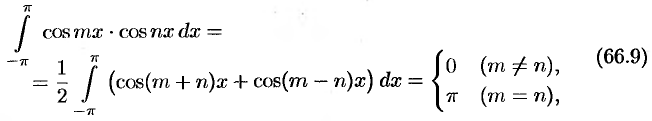
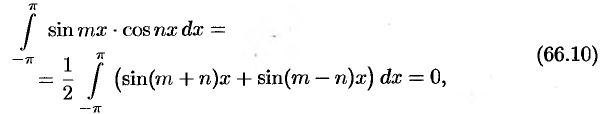
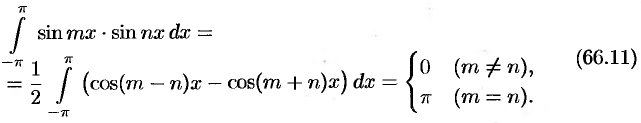
Замечания.
- Формулы (66.7) — (66.11) показывают, что семейство функций
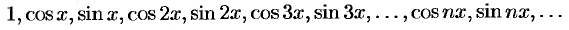обладает свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 
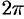, равен нулю. - Формулы (66.7) — (66.11) справедливы и в случае, когда область интегрирования есть отрезок
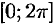(см. свойство 3 периодических функций, п. 66.1).
Пусть 
— произвольная периодическая функция с периодом 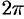. Предположим, что функция разлагается в тригонометрический ряд, т. е. является суммой рада (66.5):
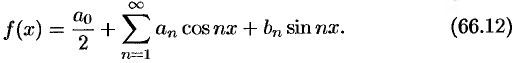
Так как функция (и сумма ряда) имеет период 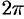, то ее можно рассматривать в любом промежутке длины 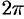. В качестве основного промежутка возьмем отрезок 
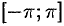(также удобно взять отрезок 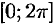) и предположим, что ряд (66.12) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты 
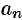и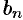 
. Для этого проинтегрируем обе части равенства (66.12) в пределах от 
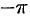до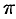 
:
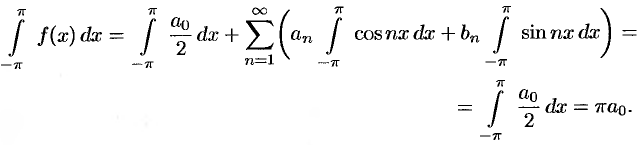
Интегралы от всех, кроме нулевого, членов ряда равны нулю в силу формул (66.7) и (66.8).
Отсюда
Умножив обе части равенства (66.12) на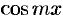 
и проинтегрировав полученный ряд в пределах от 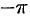до 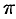, получим:
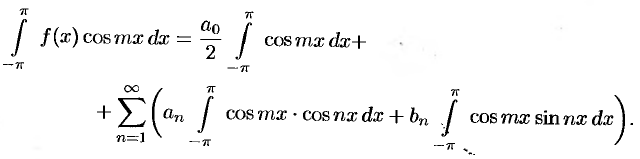
В силу формул (66.7), (66.9) и (66.10) из последнего равенства при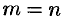 
получаем:
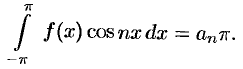
Отсюда
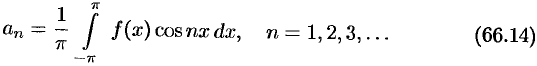
Аналогично, умножив равенство (66.12) на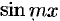 
и проинтегрировав почленно на отрезке 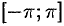, найдем:
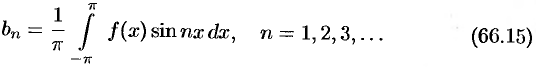
Числа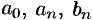 
, определяемые по формулам (66.13) — (66.15), называются коэффициентами Фурье функции , а тригонометрический ряд (66.5) с такими коэффициентами — рядом Фурье функции .
Для интегрируемой на отрезке 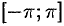функции записывают
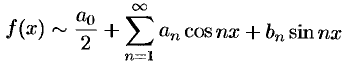
и говорят: функции соответствует (поставлен в соответствие) ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим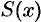 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Способ последовательного дифференцирования |
| Способ неопределенных коэффициентов |
| Разложение в ряд Фурье четных и нечетных функций |
| Разложение в ряд Фурье функций произвольного периода |
