Оглавление:
Тригонометрические подстановки
Известный приём использования различных тригонометрических подстановок применим и к целым алгебраическим уравнениям.
Пример №198.
Сколько корней на отрезке [0,1] имеет уравнение 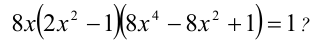
Решение:
Поскольку, по условию,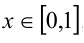 , то для любого такого x существует единственное
, то для любого такого x существует единственное 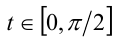 такое, что
такое, что 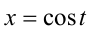 . С другой стороны, каждому
. С другой стороны, каждому 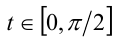 по формуле
по формуле 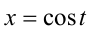 ставится в соответствие единственное
ставится в соответствие единственное 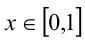 . Это означает, что между множествами значений x и t (отрезками
. Это означает, что между множествами значений x и t (отрезками 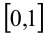 и
и 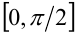 соответственно) установлено взаимно однозначное соответствие. Поэтому исходная задача сводится данной тригонометрической подстановкой
соответственно) установлено взаимно однозначное соответствие. Поэтому исходная задача сводится данной тригонометрической подстановкой 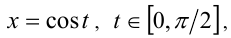 к равносильной задаче определения количества решений тригонометрического уравнения
к равносильной задаче определения количества решений тригонометрического уравнения
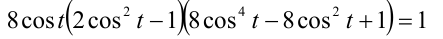
на отрезке 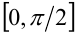 . Итак,
. Итак,
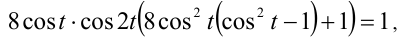
Чтобы решить полученное уравнение, его следует умножить на sin t. Проверим предварительно, будут ли значения неизвестной t, удовлетворяющие равенству sin t = 0 , решениями уравнения. Если sin t = 0 , то
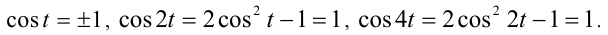
Следовательно, левая часть уравнения (1) принимает при таких t значения 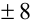 , а правая равна 1. Это означает, что все корни уравнения
, а правая равна 1. Это означает, что все корни уравнения
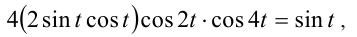
такие, что sin t = 0, будут посторонними корнями и в ответ не войдут. Несколько раз применяя формулу синуса двойного аргумента, приходим к уравнению
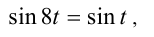
решая которое, находим две серии
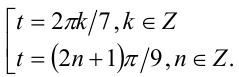
Из первой серии в отрезок 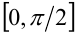 попадают два значения
попадают два значения 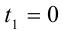 и
и 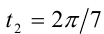 , а из второй серии — значения
, а из второй серии — значения 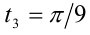 и
и 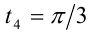 . Но
. Но 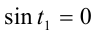 , поэтому остаётся три корня.
, поэтому остаётся три корня.
Ответ: уравнение имеет на [0,1] ровно три корня.
Замечание. Задачу можно было решить также, используя тригонометрическую замену 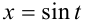 , где
, где 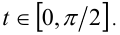
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

