Оглавление:






Тригонометрические функции
- Тригонометрическая функция. Мы уже имеем представление о тригонометрических функциях g/=zshx и y=Sozh и выраженных через них функциях,==5-1P, y=C!§х.С03,S05H31PH // = Сеч=~!- , г/=sozesx= — — — S08X31P х В этом параграфе введения мы уже объясняли определение функции g / =zsh x и логический пробел, который возникает в главе 4. Непрерывность функций Рис 4.7 G / =SOx по геометрическим
соображениям описания. Логически совершенно эти функции можно определить как решение системы из нескольких функциональных уравнений. 1)/(х1+х2)=/(х1)^(х2)+/(Х2)^(^1+л:2)=г (Х1)-Ю. Г. (Х2) — |(х1) — §(х2) — §(Х2) — § (Х2), р(х)+2(х)=Т1″О1″О1″ О1″. g (0) -1,/(y)=1. г ( — =-)=о;3)е с л и о<Х<Л -, П О<1(х)<х<Щ Х.. (4.6) _ _ 2 справедливость неравенства x< — — — 00 ■По этой причине, (4.13′))
Последнее неравенство означает последовательность в главе 3.14, благодаря принципу Людмила Фирмаль
двунаправленного ограничения (см. Главу 4, теорема 152). Непрерывность функций {181p CP/}, таким образом, последовательность{ztha}бесконечно мала. Мы докажем непрерывность функции zshx в точке x=0. Здесь мы докажем, что функция zsh x непрерывна в любой точке x бесконечной прямой. Достаточно доказать, что соответствующая последовательность{xn xn}сходится к xn xn. Давайте положим в него и используем
соотношение второго(4.10 Х2=ХП, Х1=Х.= Достаточно доказать, что правая часть (4.14) имеет элементы бесконечно малого массива,но это вскоре следует из того факта, что массив равен 181c-x. он бесконечен, благодаря уже доказанной непрерывности синуса в нуле, и ограничен последовательностью / 2soz * n * второго неравенства(4.7). 2°. Функция каждого из сегментов 81p x увеличивается с каждым из сегментов 2yl-и уменьшается с каждым из сегментов(2&+1) L-функция pops x уменьшается с каждым из сегментов K=0, —- 2Й+ — Д ( 2+1) I+ — D];
- но K-любое целое число, т. е.±1,±2,…да что с тобой такое? Д О К а з а т е л ь с т в о. найдя все монотонные области функции ZH x, мы можем получить монотонные области функции ZH x на основе уравнения (4.11), так что все аргументы будут равны функции 81p x. Кроме того, поскольку 81P x является периодической функцией 2l, следует отметить, что часть ее монотонности находится в пределах определенного периода, то есть, например, значения аргумента из отрезка.、 [2] 2] Во-первых, докажите, что функция 81p X увеличивается на сегменте пусть X1 и x2 как любые два числа из этого сегмента — Ч-ч- +— —-1- — d» — h-2——H-1-2 2 И равны второму
благодаря- Г — — — — Д, 2л — — [2] 2] °. — Что?-]• Такие, что Hg>X1. Тогда, очевидно, числа принадлежат интервалу^0, ства(4.10) 81PH2-81IH1=2CO8-B1P 2/2 (4.15}§3. Элементарная элементарная функция 153 [°- Т _ _ _ _ _ _ _ _ _ _ _ Достаточно доказать, что правая часть(4.15) имеет положительное число, и для этого для всех значений аргументов из интервала^0, для функций z t x и Sov x функция/(x)=zsh x, это следует из Свойства 3, где co8x-равенство (4.11). Таким образом, было доказано, что функция zsh x возрастает с отрезком 0″-«
■от странности функции zshx, т. е. от второго соотношения (4.8), в данном случае отрезка» -«.—-0 • таким образом, доказано, что функция 8SH x Людмила Фирмаль
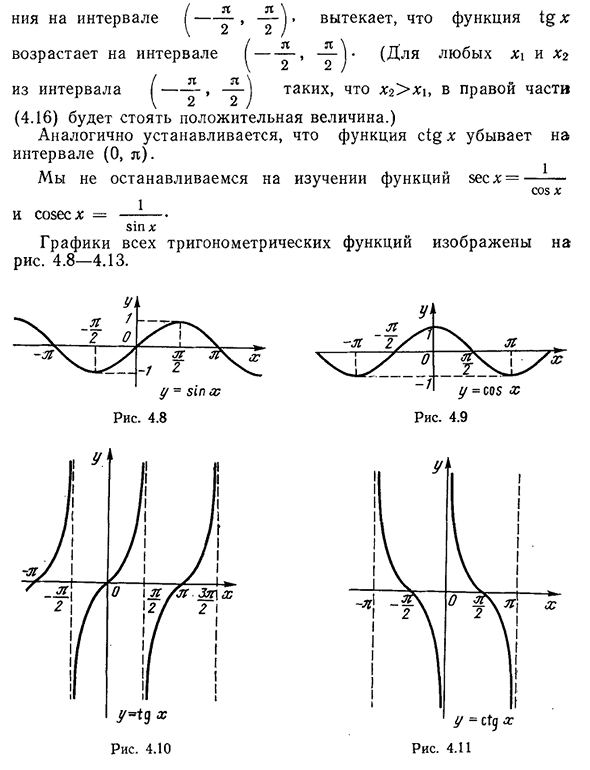
возрастает на отрезке E) остается исследовать поведение функции 81p x на отрезке. 3 1П (х+л)=8SH х-поп л+поп х-81P л=• — 81P Х. Полученное отношение, из увеличения функции 8SH x на отрезке, установленном нами, уменьшение этой функции на отрезке равно [«Tr*n+’ Исследования в области монотонности функций 8sh x и co8x были полностью завершены. _ «, 81PH, SO8H Спасибо: Shh= — — — — — -, SG§h= — — — — — — — И спасибо Х X81P соз Для частного теоремы 4.1 функция 1dx непрерывна в любой точке x=a+a функция C!§X является непрерывной в любой момент он^ыл. Используя соотношение z t (x+l)= — ZTH, co8 (x+l)= = — pop x, получим его 1C (x+l)=-8—x=1o x, а также CO8X
Смотрите также:
Методическое пособие по математическому анализу
| Степенная функция | Производные тригонометрических функций |
| Общая схема отыскания экстремумов | Обратные тригонометрические функции |

