Оглавление:
Тригонометрическая подстановка
Интегралы типа
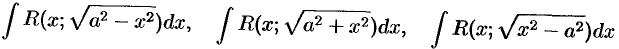
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: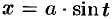 
для первого интеграла; 
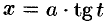для второго интеграла; 
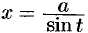для третьего интеграла.
Пример №33.6.
Найти интеграл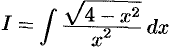 
.
Решение:
Положим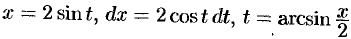 
. Тогда
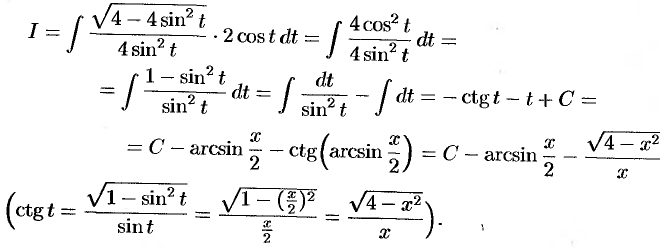
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Квадратичные иррациональности |
| Дробно-линейная подстановка |
| Интегралы типа r x (ax^2+bx+c) dx |
| Интегрирование дифференциального бинома |
