Попытаемся в записи комплексного числа 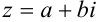 перейти от параметров
перейти от параметров 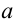 и
и 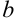 к параметрам
к параметрам 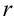 и
и 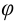 . Для этого в прямоугольном треугольнике
. Для этого в прямоугольном треугольнике 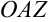 (рис. 43.1) найдем
(рис. 43.1) найдем 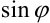 и
и 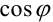 :
:
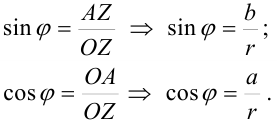
Выразим из этих формул 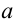 и
и 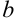 :
: 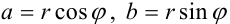 . Подставим полученные значения
. Подставим полученные значения 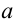 и
и 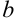 в алгебраическую форму комплексного числа
в алгебраическую форму комплексного числа 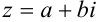 :
: 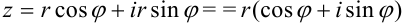 .
.
Таким образом, мы получили новую форму записи комплексного числа 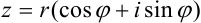 , которая называется тригонометрической формой комплексного числа.
, которая называется тригонометрической формой комплексного числа.
Пример №43.1.
Изобразите на комплексной плоскости числа: 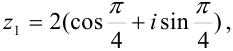
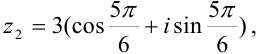
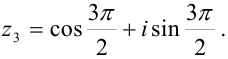
Решение:
Все числа заданы в тригонометрической форме. Выделим в записи каждого числа модуль и аргумент:
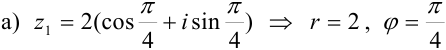 . Отложим от положительного направления оси
. Отложим от положительного направления оси 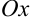 угол
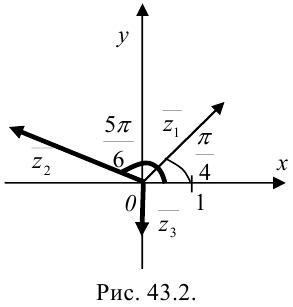
угол 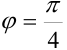 и на полученном луче отметим вектор длиной 2 ед. с центром в начале координат (рис. 43.2).
и на полученном луче отметим вектор длиной 2 ед. с центром в начале координат (рис. 43.2).
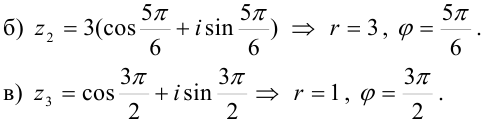
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Геометрическая интерпретация комплексных чисел. |
| Понятие модуля и аргумента комплексного числа. |
| Действия над комплексными числами в тригонометрической форме |
| Показательная форма комплексного числа. |

