Треугольники сопротивлений и тока
Если, как указано выше, все стороны треугольника напряжений разделить на величину тока, получим треугольник сопротивлений, рисунок 5.
Полное сопротивление всегда равно геометрической сумме активного и реактивного сопротивлений.

Величины 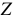 и
и 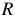 всегда положительны. Полное реактивное сопротивление
всегда положительны. Полное реактивное сопротивление 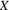 может быть как положительным, так и отрицательным. Для индуктивного характера цепи
может быть как положительным, так и отрицательным. Для индуктивного характера цепи 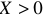 , так как
, так как 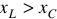 . А для емкостного характера цепи
. А для емкостного характера цепи 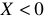 , поскольку
, поскольку 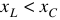 .
.
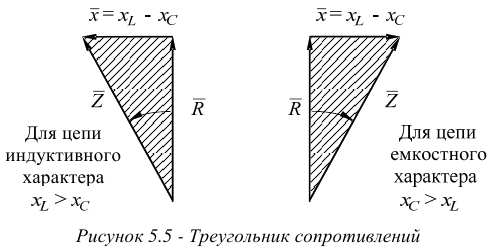
Из треугольника сопротивлений имеем:
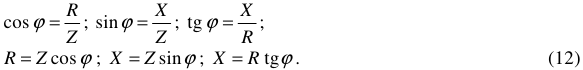
Выражения (12) используют, если заданы 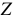 и
и 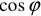 , а требуется определить
, а требуется определить 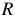 и
и 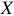 .
.
Чтобы выразить полное сопротивление комплексным числом, поместим треугольник сопротивления в комплексную плоскость.

Модуль полного сопротивления

Аргумент комплекса сопротивления

В тригонометрической и показательной формах, сопротивление можно записать таким образом:
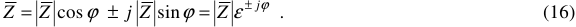
Если напряжение и ток не совпадают по фазе, то в параллельной цепи лучше раскладывать на составляющие не напряжение, а вектор тока, например, так, как показано на рисунке 6.

Общий ток всегда равен геометрической сумме активной 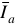 и реактивной
и реактивной 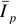 составляющих.
составляющих.
Активной составляющей называется часть общего тока, совпадающего по фазе с напряжением.
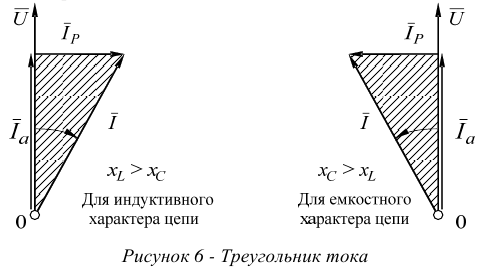
Реактивным током называется часть общего тока, сдвинутая по фазе к напряжению на угол 90° в сторону отставания или опережения.
Чтобы выразить комплексным числом треугольник тока, поместим его в комплексную плоскость.

Амперметр включенный в ветвь где протекает данный ток покажет величину равную модулю комплекса тока:

Аргумент комплекса тока,

В тригонометрической и показательной формах, ток можно записать таким образом:

Эта страница взята со страницы контрольной работы по электротехнике:
Контрольная работа по электротехнике
Возможно эти страницы вам будут полезны:
| Аналитический расчет нелинейных цепей |
| Закон Ома для полной цепи переменного тока |
| Мощность в цепи переменного тока |
| Резонанс напряжений в цепи |

