Оглавление:








Третий закон термодинамики.Тепловая теорема нернста
- Третий метод термодинамики Обсуждается Третий закон термодинамики (теорема Нернста о теплоте).Производная термодинамической величины вычисляется как Г = 0.Рассмотрен способ получения низких температур.Рассчитана постоянная давления пара.
Теорема термического Нернста Химический потенциал, необходимый для определения свободной энергии или химического равновесия, может быть рассчитан на основе количества тепла, которое может быть измерено непосредственно, например теплоты или удельной теплоты реакции.Но в то же время, некоторые очень выгодные новые принципы будут needed.As упомянутый выше максимальный объем работы L = — AG определяет химическое сродство. Член действительно состоит из 2 частей АГ = Ан-Т А5; (8.1)
- Опыт показал, что во многих случаях это делается даже при комнатной температуре.Поскольку энтропийный член T AS очень мал(особенно для реакций с участием конденсированной фазы), do ^ AN можно поместить в соответствующее приближение.На этом основано правило ленточного лота, которое гласит, что в спонтанно протекающих реакциях теплота реакции положительна.Однако это правило перестает быть справедливым, как только вклад термина-т в БС становится доминирующим.Потому что в этом случае МД может быть положительным, то есть реакция может быть эндотермической.Тогда вам нужно использовать точную формулу (8.1).
При достаточно низких температурах последний срок должен быть незначительным. Людмила Фирмаль
До сих пор мы только предполагаем конечность значений в DS, но это уже Лим АГ = АП. (8.2) р-> о Однако, в зависимости от многочисленных тщательных измерений значений AG и AJ, Нернст(1906) представил гораздо более сильное предположение, предполагая, что не только T A5, но и величина AS исчезает с абсолютным нулем[25]. «Для всех изменений, происходящих в чистой конденсированной материи при абсолютном нуле, изменение энтропии равно нулю.»Поэтому、 Лим как-0 при T — >0.(8.3)) Как видно из Формулы (8.1), это также、 Лим АГ〜а // = 0 при T — > 0, (8.4) Или молекулы стремятся к нулю быстрее, чем Т. Прежде чем перейти к результатам теоремы Нернста, обратимся к выводу об асимптотическом законе при низких температурах, не прибегая к новым принципам.
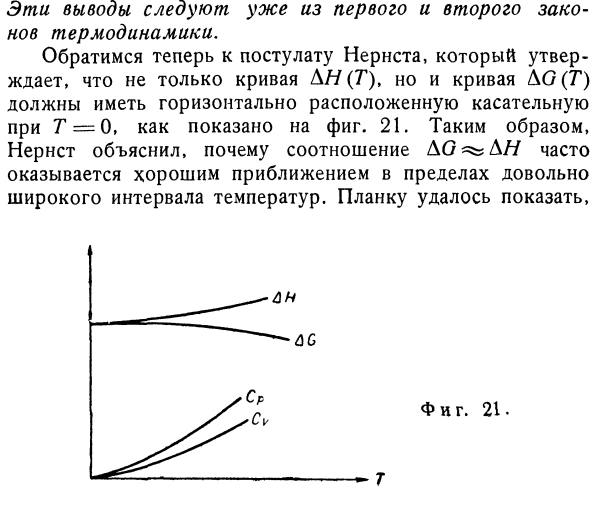
Из уравнения Гиббса Гельмгольца 、 а. АГ-ИИ .. ДГ Т Л / О Р / ч. Лим-Джей-= Лим-> г —> 0. (8.5) Когда вы применяете правило роспиталь, левая сторона .. Г ДГ ДГ, ДНЛ П / 0 Лим хромает. (8.6) Таким образом, с абсолютным нулем, для всех систем Для гамма — > 0, lim Cp =0.(8.7) Аналогично, используя уравнение Гиббса Гельмгольца, связывающее F и U、 Лим СV = 0, а — > 0. (8.8) Эти выводы получены уже из первого и второго законов термодинамики. Теперь обратимся к предположению Нернста.Это означает, что не только кривая D //(G), но и кривая AG(G)должны иметь горизонтальные касательные с Г= 0. 21.Поэтому Нернст объяснил, почему отношение DO ^ D //часто является хорошим приближением в довольно широком диапазоне температур.Я могу показать тебе Планк.
И фигура тоже. 21. Предположение Нернста тесно связано с квантовой теорией, и фактически оно говорит, что оно является одним из ее результатов.Более глубокий анализ является задачей статистической механики, но мы рассмотрим основные идеи Нернста. Принцип Больцмана формулировки планка(см. Главу 2,§ 5), где S =W Состояние, соответствующее этому термодинамическому состоянию.В отличие от классического механического состояния, которое образует континуум, квантовое состояние дискретно, и при абсолютном нуле система находится в самом низком квантовом state.So, в процессе абсолютного нуля температура равна W-1, 5 = 0 и даже D5 = 0. Хотя утверждение о том, что W = 1 верно для состояния с наименьшей энергией, приведенное выше»доказательство» теоремы Нернста о теплоте, основанное на квантовой теории, является неполным.
- Новый курс доказательства был подробно разработан Казимиром в статье, включенной в Книгу, данную Крамерсом несколько лет назад и посвященную 80-летию Макса Борна (см.[26]). Фактически дискретность энергетического уровня, принятая в квантовой теории, лишь косвенно связана с тенденцией энтропии к нулю.
Точнее, дискретность уровня сама по себе не означает, что уменьшение энтропии может быть заметно при температурах, достижимых в эксперименте.Даже самая низкая температура, достигнутая в эксперименте, не может вообще утверждать, что система находится в этом самом низком квантовом состоянии.Тем не менее, экспериментально измеренная кривая D5 (D) стремится к нулю по мере снижения температуры, экстраполируя из экспериментально достижимой температуры.
Плотность уровней всех известных систем стремится к нулю с уменьшением энергии, так как при этих температурах энтропия стремится к нулю.Более подробный анализ читатель найдет в исследовании Кашмира (см. Также[27]).
Объяснение заключается в том, что асимптотический закон термодинамики, такой как—> 0, определяется плотностью энергетического уровня, которая близка к состоянию наименьшей энергии. Людмила Фирмаль
Поскольку существуют метастабильные состояния и вырожденные состояния с наименьшей энергией, мы не всегда можем применить теорему Нернста в предельной форме, предложенной Планком. Для гамма — > 0, limS =0.(8.9) Однако теорему Нернста можно связать со следующими феноменологическими принципами: Нет такой системы, которая могла бы остыть до абсолютного нуля. В качестве формулировки третьего закона термодинамики рекомендуется взять это следствие из теоремы Нернста.
Смотрите также:
| Закон действующих масс | Недостижимость абсолютного нуля |
| Химическое сродстово | Постоянная давления пара |

