Оглавление:













Трение скольжения несмазанных тел
- А. Направление и величина силы трения. Коэффициент трения Опыт показывает, что сила трения на поверхности соприкосновения двух твердых тел всегда направлена в сторону, обратную относительной скорости движения или, если оба тела находятся в покое, в сторону, обратную силе, стремящейся привести в движение одно из соприкасающихся тел. Величина силы трения зависит от многих факторов, учет которых представляет значительные трудности. Во многих случаях с доста-Трение скольжения несмазанных тел 125 точной для практических целей точностью при определении величины силы трения можно пользоваться установленной Кулоном формулой F = fQ, (6) Q противодействует сила 2 Фиг. 125. где F — сила
трения, Q — нормальная к поверхности соприкосно’ вения сила, с которой тело/ прижато к телу 2 (фиг. 125), и f — коэффициент пропорциональности, называемый коэффициентом трения скольжения. Таким образом, если тело/ движется относительно тела 2 с некоторой скоростью и12, то такому движени трения F, направленная в сторону, обратную скорости и12, и определяемая по формуле (6). Опыт показывает, что при одних и тех же телах / и 2, при одной и той же силе Q и при прочих одинаковых условиях сила трения Fo , которую необходимо преодолеть, чтобы привести в движение одно из находящихся в покое тел относительно другого, оказывается больше той силы трения F, которая
противодействует телу / при его движении относительно тела 2. Поэтому при Людмила Фирмаль
определении силы трения по приведенной выше формуле необходимо учитывать разницу между величинами коэффициента трения скольжения f и коэффициента трения покоя /0. Так как сила трения является силой реактивной, то определенная по формуле (6) величина Q/o силы трения покоя является наибольшей возможной, могущей оказать сопротивление силе Р, стремящейся сдвинуть одно из соприкасающихся тел относительно другого, но при Р < Q/o сила трения равна точно силе Р. Коэффициент трения скольжения является безразмерной величиной, которая приводится в инженерных справочниках для разных частных случаев, где
учитываются только материалы трущихся тел и чистота обработки их соприкасающихся поверхностей. Пользуясь справочной величиной коэффициента трения и определяя величину силы трения по. приведенной выше формуле, мы будем предполагать, что величина коэффициента трения зависит только от материала и чистоты поверхности и не зависит ни от скорости скольжения, ни от удельного давления, ни от времени, в течение которого скольжение совершается. Следует иметь в виду, что такое предположение будет верным лишь приблизительно и только в пределах скоростей скольжения, удельных давлений и длительности скольжения,
- использованных Кулоном при опытах, на основании которых была установлена указанная формула. Пределы, в которых производились опыты Кулоном в 1785 г. и Мореном, проверявшим опыты Кулона в 1834 г., были следующими: скорость скольжения — от 0,3 до 3 м/сек, давление на поверхности соприкосновения — не больше 10 кг/см2. Это надо иметь в виду, потому что в современной технике часто126 Трение в кинематических парах приходится иметь дело со значительно большими скоростями и давлениями на поверхностях трения. Длительность скольжения в опытах Кулона вовсе не принималась во внимание. Опытами, которые производились разными исследователями после опытов Кулона и Морена, было
установлено, что за указанными пределами величина коэффициента трения изменяется, и притом значительно, и от скорости скольжения, и от давления на поверхности трения, и от длительности скольжения. Так например, было установлено, что при увеличении скорости скольжения от 2,13 до 26,8 м/сек величина коэффициента трения уменьшалась почти в 6 раз, а при одной и той же скорости уменьшалась почти в 3 раза через 25 сек. после начала опыта. Изложенное выше необходимо иметь в виду при определении величин сил трения в технических расчетах, основанных на использовании справочных данных о величинах коэффициентов трения. Б. Угол и конус трения Если тело/ (фиг. 126)
прижато к телу 2 силой Q12, то при отсутствии силы трения реакция Q?1 со стороны Людмила Фирмаль
тела 2 на тело / направлена Фиг. 126. по нормали к поверхности соприкосновения. При наличии силы трения F реакция R является равнодействующей нормальной реакции Q2l и силы трения F. Угол <р, на который равнодействующая R отклоняется от нормальной реакции Q2i, называется углом трения. Из фиг. 126 следует, что Поэтому в соответствии с уравнением (6) получаем tg <р = А (7) т. е. коэффициент трения равен тангенсу угла трения. Итак, у г л о м т р е н и я называется угол между нормальной реакцией и равнодействующей силы трения и нормальной реакции или, говоря иначе, угол, тангенс которого равен коэффициенту трения.Трение скоЛьжения несмазанных тел 127 При движении тела 1 в разных
направлениях по плоскости равнодействующая R реакций будет отклоняться от нормальной реакции Q21 на угол в сторону, обратную относительной скорости движения, оставаясь всегда на поверхности конуса с углом 2<р при вершине, образованного вращением равнодействующей R вокруг нормальной реакции (фиг. 127). Такой конус называется конусом трения. Иначе, к о н у с о м т р е н и я называется поверхность, описанная равнодействующей силы трения и нормальной реакции при вращении ее вокруг нормальной реакции, или, конус с углом при вершине, равным двойному углу трения. В. Трение на горизонтальной плоскости Движение тела на плоскости можно рассматривать под действием . только одной силы,
так как во всех случаях несколько действующих на тело сил могут быть приведены к одной равнодействующей. Предположим, что на тело действует сила Q (фиг. 128) под углом X к перпендикуляру к плоскости соприкосновения. Перенесем силу Q в точку пересечения ее вектора с перпендикуляром к плоскости соприкосновения и разложим ее по двум взаимноперпендикулярным направлениям. Нормальная составляющая Qn , прижимая тело к плоскости, создает противодействующую движению тела силу трения покоя Fo ; тангенциальная составляющая Q’ стремится сдвинуть тело. Для возможности движения необходимо соблюдение следующего условия: ФТ >Л>Так как Q’ = Qsin К, = f0Qn = f0Q cos X, где /о — коэффициент трения покоя, то Qsin X > f 0Qcos X, откуда tg X > / 0 или на основании формулы (7) tg X > tg <р0; X > <Ро> где <р0 — угол трения
покоя.128 Трение в кинематических парах Из этого следует, что сила, действующая внутри конуса трения, независимо от ее величины, привести в движение тело не может. Подставив в приведенные выше неравенства F вместо Fo , f и ? вместо /0 и % и заменив во всех неравенствах знак > знаками > , придем к заключению, что движение тела на горизонтальной плоскости возможно лишь при соблюдении условия X > <р. При X = <р получаем QT — F и движение с постоянной скоростью, при X > ср получаем QT > F и движение с ускорением. При X < ср0 возникновение движения, как было показано выше, невозможно; при X < ср вызванное какими-либо силами и продолжающееся по инерции движение тела при действии на него силы Q будет происходить с замедлением, так как в этом случае
создаваемая силой Qn противодействующая движению сила трения будет больше силы Qx , поддерживающей движение. Из изложенного выше следует, что вопросы о возможности возникновения движения одного из соприкасающихся тел относительно другого и о возможности движения с постоянной скоростью или ускорением разрешаются одинаково с той только разницей, что в одном случае приходится принимать во внимание коэффициент /0 и угол <р0 трения покоя, а в другом — коэффициент f и угол <р трения скольжения. Г. Трение на наклонной плоскости Рассмотрим сначала случай, когда на тело, находящееся на плоскости, наклоненной под
углом X к горизонту, действует одна сила, перпендикулярная к основанию плоскости (фиг. 129), например сила веса. В таком случае движение возможно только вниз. Угол между вектором силы Q и перпендикуляром к плоскости равен углу X наклона плоскости. В соответствии с изложенным выше для возможности движения необходимо соблюдение условия X > ср. При X < ср под действием силы, перпендикулярной к основанию плоскости, движение независимо от величины силы не может ни возникнуть, ни продолжаться без замедления. Плоскость с углом наклона, меньшим угла трения, называется с а м о т о р м о з я щ е й . Явление
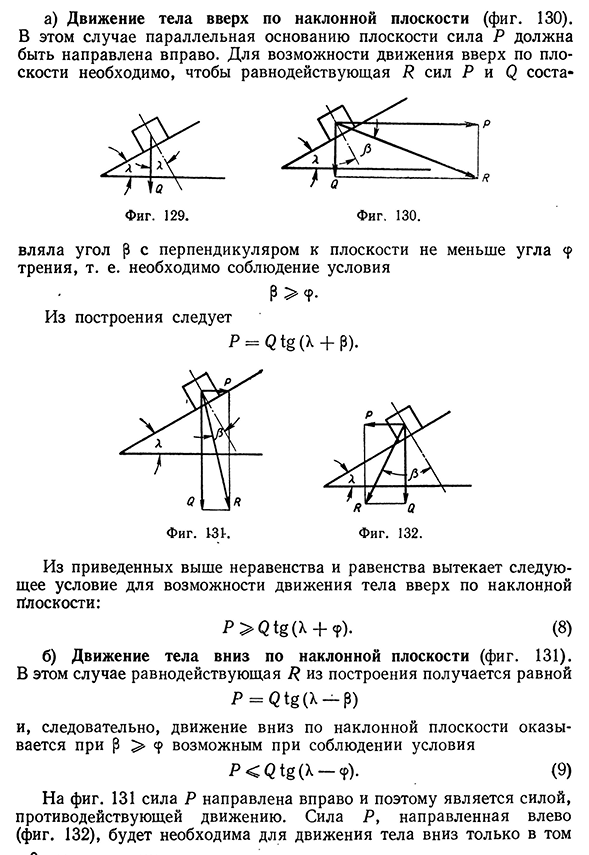
самоторможения весьма широко используется в технике в разнообразных устройствах. Рассмотрим теперь случай, когда на тело, находящееся на плоскости, наклоненной под углом X к горизонту, действуют две силы, одна из которых перпендикулярна, а другая параллельна основанию плоскости. В этом случае движение тела возможно в обоих направлениях. Выясним условия для возможности движения в каждом из двух направлений.Трение на наклонной плоскости L4.ZJ а) Движение тела вверх по наклонной плоскости (фиг. 130). В этом случае параллельная основанию плоскости сила Р должна быть направлена вправо. Для возможности движения вверх по плоскости необходимо, чтобы равнодействующая R сил Р и Q составляла угол р с перпендикуляром к плоскости не меньше угла <р трения, т. е. необходимо соблюдение условия ₽ > ? • Из построения следует P = Q
tg(k + ₽). Из приведенных выше неравенства и равенства вытекает следующее условие для возможности движения тела вверх по наклонной плоскости: P > Q tg ( k + ?). (8) б) Движение тела вниз по наклонной плоскости (фиг. 131). В этом случае равнодействующая R из построения получается равной P = Q tg ( X ₽ ) и, следовательно, движение вниз по наклонной плоскости оказывается при р > <р возможным при соблюдении условия P < Q t g ( k ? ). (9) На фиг. 131 сила Р направлена вправо и поэтому является силой, противодействующей движению. Сила Р, направленная влево (фиг. 132), будет необходима для движения тела вниз только в том 9 Зиновьев 612130 Трение в кинематических парах случае, если под
действием только одной силы Q движение не будет происходить, т. е. в случае X < ср. Из построения (фиг. 132) получаем P = Q tg (₽ -X ). При р > ср и указанном на фиг. 132 направлении силы Р необходимая величина силы Р должна удовлетворять условию р >Q tg(cpх). (Ю) Д. Трение клинчатого ползуна Выше во всех тело к плоскости случаях предполагалось, что сила, прижимающая трения, направлена перпендикулярно к этой плоскости. В таких случаях в соответствии с уравнением (6) величину силы трения мы получали, умножая силу, Фиг. 134. прижимающую тело к плоскости, на коэффициент трения. На фиг. 133 изображен клинчатый ползун, имеющий в поперечном сечении форму трапеции, который прижимается силой Q к двум поверхностям трения, наклоненным каждая к линии действия сил
ы Q под углом 7. При движении клинчатого ползуна в направлении, перпендикулярном к плоскости чертежа, величина силы трения в соответствии с формулой (6) получается равной F = 2Nf, где N — сила, перпендикулярная к плоскости трения. Приняв во внимание, что сумма проекций сил на вертикаль равна нулю, получаем Введя обозначение — получаем F = Qf’, (И) где величина f’ называется фиктивным или приведенным коэффициентом трения. С фиктивным коэффициентом трения, а также с фиктивным углом трения ср’, определяемым из равенства tg <р’ — f , в технических расчетах
приходится иметь дело в тех случаях, когда сила, прижи-Трение в винтах 131 мающая одно тело к другому, направлена не по нормали к поверхности трения. Так как f’ > f, то в тех случаях, когда при определенной силе, прижимающей одно тело к другому, желательно получить возможно большую силу трения, поверхности трения располагают иногда не под прямым углом к линии действия прижимающей силы. Например, для уменьшения силы, прижимающей одно из фрикционных колес к другому, ободы колес иногда делают клинчатыми (фиг. 134). С другим примером мы
встретимся в следующем пункте настоящего параграфа. Если вместо клинчатого ползуна, движущегося в направлении, перпендикулярном к плоскости чертежа, представить себе сплошной усеченный конус (фиг. 133), прижимаемый силой Q к внутренней поверхности полого усеченного конуса, то величину силы трения, противодействующей вращению сплошного конуса в полом, надо будет определять также по уравнению (11). прямой (фиг. 135) Е. Трение в винтах При определении величины силы трения на поверхности соприкосновения винта и гайки предполагается, что развернутая винтовая поверхность винта представляет собой наклонную плоскость с гайкой в виде груза на наклонной плоскости или, наоборот, что наклонной плоскостью является развернутая винтовая поверхность гайки, а винт представляет собой груз на этой наклонной плоскости. Делая такое предположение, следует иметь в виду, что развернутая винтовая поверхность на самом деле не представляет собой наклонной плоскости с определенным углом наклона. Винтовую поверхность мы получим, двигая отрезок Л В
точкой А по винтовой линии и удерживая его при этом движении нормально к поверхности цилиндра или, что одно и то же, перпендикулярно оси цилиндра. За один оборот вокруг оси цилиндра, когда отрезок А В перейдет в положение A ]B lt все точки отрезка продвинутся вдоль оси цилиндра на один и тот же шаг t, но все точки пройдут пути по цилиндрам с разными диаметрами: одна крайняя точка А отрезка пройдет по цилиндру с диаметром di, другая крайняя точка В — по не изображенному на фиг. 135 цилиндру с диаметром d. Угол Хл подъема винтовой линии, по которой пройдет точка Л, будет равен XA = arctg-^-, угол подъема винтовой 1 ( линии, по которой пройдет точка В, будет равен лв = a r c t g ^ -. Так как dt < d, то Хл > Хв . Предположив, что развернутая винтовая поверхность представляет собой наклонную плоскость с одним определенным углом наклона — углом Хл или мы допустим неточность, которая не 9132 Трение в
кинематических парах будет иметь практического значения, если длина отрезка АВ будет мала по сравнению с диаметром d± или d, что в машиностроении почти всегда и имеет место. Еще меньшую неточность мы допустим, если будем предполагать, что развернутая винтовая поверхность представляет собой наклонную плоскость с углом наклона, равным углу подъема винтовой линии на среднем диаметре, т. е. углу, определяемому по уравнению Х = + d ’ Я 2 Винтовую резьбу на винте можно представить себе получающейся при движении точек А и A i профиля резьбы в виде прямоугольника Фиг. 136. Фиг. 137. Фиг. 138. A B B iA i (фиг. 136) или треугольника A B A i (фиг. 137) вдоль винтовых линий, расположенных на цилиндре с диаметром dx; при таком движении отрезок ЛЛХ должен оставаться все время параллельным оси цилиндра. Практически винтовая резьба получается, разумеется, путем удаления материала с цилиндра
диаметром d при помощи режущего инструмента. Подобным же образом можно представить себе образование и практическое получение винтовой резьбы гайки. Развертывая мысленно соприкасающиеся поверхности винта и гайки и представляя себе одно из звеньев винтовой пары в виде наклонной плоскости, мы можем считать другое звено сосредоточенным грузом на этой плоскости, исходя из того, что согласно формуле (6) сила трения не зависит от величины поверхности соприкосновения. Поступая таким образом, мы можем пользоваться формулами (8), (9) и (10), устанавливающими зависимости между силами Р и Q, действующими на тело, находящееся на наклонной плоскости. При
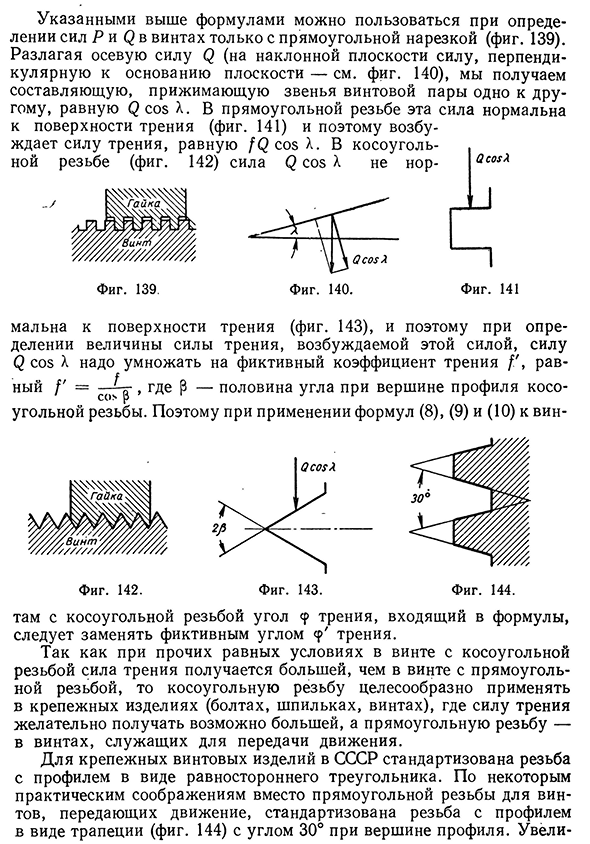
применении этих формул к винтовой паре углом X в этих формулах будет угол подъема винтовой линии на среднем диаметре, силой Q — сила, направленная по оси пары, силой Р — сила, направленная по касательной к окружности с радиусом, равным среднему радиусу винтовой резьбы. Если г — средний радиус винтовой резьбы и М — момент, вращающий подвижное звено винтовой пары (винт или гайку), то Р = — . Например, если Ро — сила, которую прикладывает рабочий к гаечному ключу при завертывании или отвертывании гайки (фиг. 138), I — расстояние от точки приложения силы Р о до оси винтовой пары, то Р = Р о .Трение в винтах 133 Указанными выше формулами можно пользоваться при определении сил Р и Q в винтах только с прямоугольной нарезкой (фиг. 139). Разлагая осевую силу Q (на наклонной плоскости силу, перпендикулярную к основанию
плоскости — см. фиг. 140), мы получаем составляющую, прижимающую звенья винтовой пары одно к другому, равную Q cos X. В прямоугольной резьбе эта сила нормальна к поверхности трения (фиг. 141) и поэтому возбутрения (фиг. 143), и поэтому при опретрения, возбуждаемой этой силой, силу мальна делении Q cos X ный f’ = , где р — половина угла при вершине профиля косоугольной резьбы. Поэтому при применении формул (8), (9) и (10) к вин к поверхности величины силы надо умножать на фиктивный коэффициент трения равf COS Р там с косоугольной резьбой угол трения, входящий в формулы, следует заменять фиктивным углом <р’ трения. Так как при прочих равных условиях в винте с косоугольной резьбой сила трения получается большей, чем в винте с прямоугольной резьбой, то косоугольную резьбу целесообразно применять в
крепежных изделиях (болтах, шпильках, винтах), где силу трения желательно получать возможно большей, а прямоугольную резьбу — в винтах, служащих для передачи движения. Для крепежных винтовых изделий в СССР стандартизована резьба с профилем в виде равностороннего треугольника. По некоторым практическим соображениям вместо прямоугольной резьбы для винтов, передающих движение, стандартизована резьба с профилем в виде трапеции (фиг. 144) с углом 30° при вершине профиля. Увели-134 Трение в кинематических парах чение силы трения по сравнению с
прямоугольной резьбой в трапецеидальной резьбе получается незначительным, так как косинус половины угла при вершине профиля получается близким к единице (cos 15° = 0,966), а поэтому и разница между коэффициентами /’ и f получается незначительной (/’ 1,03/). В метрической резьбе (так называется стандартная резьба для крепежных изделий) угол при вершине профиля равен 60°, следовательно, « г яF1 > ш г с ни ’) н J ■) ж L □ В крепежных винтовых изделиях резьба должна быть обязательно самотормозящей, иначе такие изделия не могли бы выполнять своего назначения. Уясним теперь себе, как, пользуясь формулами (8), (9) и (10), можно решать вопросы о величинах сил, действующих на болт с гайкой при монтаже болта. При соединении болтом деталей Л и В (фиг. 145, а) болт вставляется в отверстия этих деталей, затем на верхнюю
нарезанную часть болта навертывается гайка. Пока гайка не дошла еще до детали Л, резьба неподвижного болта представляет собой как бы наклонную плоскость, навернутую на цилиндр, а гайка — груз на этой плоскости, перемещаемый при положении болта, показанном на фиг. 145, а, сверху вниз. Оставленная в каком-либо положении, например в изображенном на фиг. 145, а, гайка не перемещается книзу под действием собственного веса, потому что треугольная резьба болта самотормозящая, т. е. удовлетворяющая условию X < ср’. Для того, чтобы привести в соприкосновение нижнюю поверхность ab сайки с верхней поверхностью cd детали А, необходимо вращать гайку моментом Рг, где г — средний радиус резьбы, Р — сила, приведенная к среднему радиусу и определенная по формуле (10), в которой вместо
угла <р трения подставлен фиктивный угол <р’ трения, а силой Q является незначительный вес гайки. Небольшой момент, необходимый для движения гайки до детали А, создается обычно пальцами рабочего. Когда нижняя поверхность гайки совмещена с верхней поверхностью детали А, то для дальнейшего вращения гайки с целью затягивания болта требуется значительно больший вращающий момент. Вращаясь, гайка должна передвигаться по болту в изображенном на фиг. 145, б положении вниз, а этому препятствует деталь Л, в которую гайка уже упирается. Вращаясь и оставаясь в соприкосновении с деталью Л, гайка могла бы перемещаться относительноТрение в винтах 135 болта вниз, если бы
болт мог перемещаться вверх, но этому препятствует деталь В, в которую болт упирается головкой. Дальнейшее вращение гайки на некоторый угол является все-таки возможным и при монтаже болта обязательно производится. При этом вращении гайка, упираясь нижней своей поверхностью в деталь А и действуя витками своей резьбы на резьбу болта, растягивает болт, незначительно увеличивая его длину. На этой стадии роли болта и гайки меняются: гайка становится как бы наклонной плоскостью, а болт — грузом, перемещаемым вверх по наклонной плоскости. При растягивании болта происходит в основном то же, что происходило бы в устройстве, схематически изображенном на фиг. 146, если бы
аналогичный болту груз Q, который может перемещаться только в вертикальном направлении, перемещался бы деталью Г, аналогичной гайке. Действуя с некоторой силой Р т, направленной на фиг. 146 справа налево, можно поднять груз Q (на фиг. 145, б растянуть болт с силой Q), переместив груз в то же время относительно детали Г слева направо (аналогично вращению гайки относительно болта на фиг. 145, б). На фиг. 146 сила Р т должна преодолеть сопротивление груза Q и силы трения на наклонной плоскости и, кроме этого, силу трения на горизонтальной плоскости соприкосновения деталей А и Г. Необходимую силу для перемещения груза Q относительно детали Г вправо надлежит определять по формуле (8); сила трения на плоскости соприкосновения деталей А и Г равна Qf (вес детали Г не принимается во внимание). Поэтому ^m = Qtg(X + гДе ? г — сила на
среднем радиусе резьбы и Q — сила, растягивающая болт, а также момент QfR силы трения на плоскости соприкосновения гайки и детали А , где R — радиус окружности, на которой можно считать приложена равнодействующая элементарных сил трения (определение величины см. ниже в п. «3»). Затянутый гаечным ключом болт остается в растянутом положении в напряженном состоянии, потому что при самотормозящей резьбе под действием осевой силы он не может повернуться в гайке и таким образом вернуться к исходному положению.136 Трение в кинематических парах При демонтаже соединения необходимо вращать гайку
моментом M > Q r tg (ср’— К) + где фр — фиктивный угол трения покоя в резьбе и /0 — коэффициент трения покоя между гайкой и деталью А. Ж Трение во вращательных парах Вращательная кинематическая пара образуется цапфой (опорной частью вала) и охватывающим ее подшипником. Для того чтобы цапфа, находящаяся под действием нескольких приложенных к ней сил могла вращаться, необходимо, чтобы равнодействующая Q этих сил (фиг. 147) создавала момент, не меньший момента силы трения. Разложив силу Q на нормальную Q» и тангенциальную QT составляющие и обозначив через г плечо силы Q относительно оси вращения цапфы, через 7? — радиус цапфы и через X — угол между линией действия силы Q и радиусом, проведенным в точку приложения силы Q, получим:
момент, вращающий цапфу, равен QXR = QR sin К ; момент силы трения F равен F7? = fQnR = QRf cos X = QR tg ср cos X. Для возможности вращения необходимо соблюдать условие QR sin X > QR tg <р cos X, откуда tg X > tg ср; X >ср и поэтому г = R sin X > R sin <р. Следовательно, момент силы Q не может вращать цапфы, если линия действия силы Q проходит внутри круга с радиусом R sin ср. Такой круг называется к р у г о м т р е н и я . 3. Трение в пятах Трение в пятах имеет место на поверхности соприкосновения двух прижатых одно к другому тел, вращающихся одно относительно другого вокруг нормали к поверхности соприкосновения (фиг. 148).Трение в пятах 137 При учете сопротивления, оказываемого силами трения моменту, вращающему одно тело относительно другого, приходится определять
равнодействующий момент сил трения, заменяя элементарные силы трения на всей поверхности трения равнодействующей силой, приложенной на окружности с радиусом /?. Определим величину радиуса предположив, что поверхность трения представляет собой кол ьцевую площадь с внешним радиусом и внутренним радиусом г2 и что вращение происходит вокруг общего центра окружностей с этими радиусами ———— — — (фиг. 149).. Полная сила трения скольжения равна ( d d ) , где р — давление на поверхности трения, т.
е. сила, приходящаяся на единицу поверхности трения, те (rf — — величина верхности трения. Элементарная сила щадью 2теп/г, равна и поФиг. 148. трения, 7 — ) Фиг. 149. распределенная по кольцу с плоpfS^rdr. Момент полной силы трения где 7? — радиус окружности, на которой приложена равнодействующая элементарных сил трения. Этот же момент может быть выражен и следующим образом: J pf2nr2dr = 2р/те J r2dr. Гя гг Приравнивая и сокращая на р/те, получаем уравнения: (г2 — г|) 7? = 2 J r2dr; Гя ( ‘ • i i ) ^ = 4 ( r i r 23) > откуда р 2 г 1 ~ г2 2 d + V z + d К я = 3 г2 _ г2 3 Г1 + г2 При г» = 0 получаем
Смотрите также:
| Виды трения | Трение скольжения смазанных тел |
| Определение основных размеров маховика двигателя | Трение гибких тел |

