Оглавление:









Трение качения
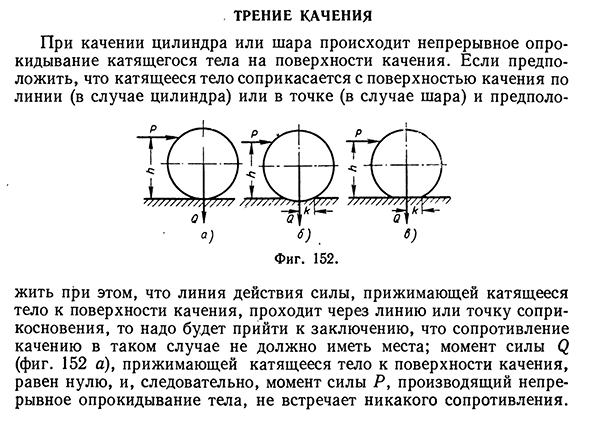
- При качении цилиндра или шара происходит непрерывное опрокидывание катящегося тела на поверхности качения. Если предположить, что катящееся тело соприкасается с поверхностью качения по линии (в случае цилиндра) или в точке (в случае шара) и предположить при этом, что линия действия силы, прижимающей катящееся тело к поверхности качения, проходит через линию или точку соприкосновения, то надо будет прийти к заключению, что сопротивление качению в таком случае не должно иметь места; момент силы Q (фиг. 152 а), прижимающей катящееся тело к
поверхности качения, равен нулю, и, следовательно, момент силы Р, производящий непрерывное опрокидывание тела, не встречает никакого сопротивления.142 Трение в кинематических парах Между тем опыт показывает, что сопротивление качению имеет место. Сопротивление качению возникает потому, что тела, прижимаемые одно к другому некоторой, хотя бы и незначительной силой, деформируются и в деформированном состоянии соприкасаются не по линии или в точке,
а по некоторой поверхности, примыкающей к линии или точке. При деформации поверхности под катящимся Людмила Фирмаль
телом (фиг. 152, б) и при деформации катящегося тела (фиг. 152, в), а следовательно, при деформации и тела и поверхности одновременно линия или точка, около которой происходит опрокидывание, отходит на некоторое расстояние k от линии действия силы Q. Вследствие этого создается плечо k силы Q и момент Qk, противодействующий опрокидывающему моменту Ph. При качении с постоянной скоростью должно иметь место очевидное соотношение Ph = Qk, где k — величина, характеризующая условия, при которых происходит качение; она называется к о э ф ф и ц и е н т о м т р е н и я к а ч е н и я. В отличие от коэффициента трения скольжения коэффициент трения качения является величиной с линейной размерностью. Явление качения наблюдается благодаря наличию трения скольжения:
качение одного тела по другому может происходить только в том случае, если сопротивление скольжению превышает сопротивление качению. Для того, чтобы заставить тело катиться по плоскости, надо приложить к телу силу, равную а для скольжения необходимо приложить силу, равную Pc = Qf-Если и, следовательно, Рк < Рс, то тело будет катиться без скольжения, в противном случае тело будет скользить без качения. При — f будет одинаковая возможность и качения и скольжения. Так как при замене трения скольжения трением качения сила трения уменьшается и в большинстве случаев значительно, то при передвижении по плоскости грузов является
- целесообразным подкладывать под грузы катки в виде цилиндрических стержней или обрезков труб, что часто и делается. При передвижении груза весом Q на катках с радиусами R (фиг. 153) преодолеваются силы трения качения между грузом и и катками и между катками и плоскостью. В этом случае действую-Трение качения 143 щая на груз сила Р оказывается приложенной к каткам в точках их соприкосновения с грузом и создает момент P2P, вращающий катки. Сопротивление качению оказывается моментами — kx и ( 4 ’ + ° ) ^ ’ где G — вес катка; п — число катков; k2 и kY — коэффициенты трения качения между катками и плоскостью и между катками и грузом соответственно При движении с постоянной скоростью получаем 2РР — п п + G k 2 = + (Q + ^G) k2. При k\ = k2 = k, пренебрегая весом катков, получаем ^ 4 Так как катки относительно груза перемещаются в сторону, обратную направлению движения
груза, то уходящие из-под груза катки приходится под груз вновь подкладывать, что делает неудобным перемещение груза на катках на большое расстояние или с большой скоростью. При передвижении груза на колесах (фиг. 154) колеса увлекаются (нагруженным кузовом тележки, ’ но так как колеса вращаются на осях, связанных с грузом, то, кроме силы трения качения между колесами и плоскостью, при движении груза преодолевается и сила трения скольжения между колесами и осями, на которых они вращаются. При передвижении груза с постоянной скоростью моменту РР силы Р, которую следует считать приложенной на расстоянии Р от плоскости по линии действия параллельной плоскости, противодействуют:
1) момент силы трения качения (Q + G) k, где G —144 Трение в кинематических Людмила Фирмаль
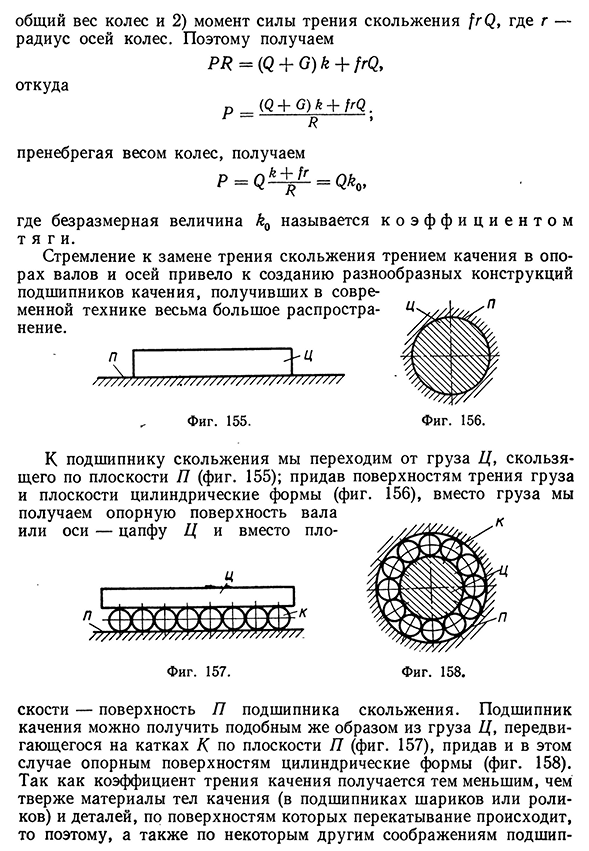
парах общий вес колес и 2) момент силы трения скольжения frQ, где г — радиус осей колес. Поэтому получаем p ^ = = (Q + G )& +/rQ , откуда п _ (Q + G) & + frQ. г ~ Я пренебрегая весом колес, получаем P = Q ^ = Qo> где безразмерная величина kQ называется к о э ф ф и ц и е н т о м т я г и. Стремление к замене трения скольжения трением качения в опорах валов и осей привело к созданию разнообразных конструкций подшипников качения, получивших в современной технике весьма большое распространение. Фиг. 155. Фиг. 156. К подшипнику скольжения мы переходим от груза Ц, скользящего по плоскости П (фиг. 155); придав поверхностям трения груза и плоскости цилиндрические формы (фиг. 156), вместо груза мы получаем
опорную поверхность вала или оси — цапфу Ц и вместо плоФиг. 158. скости — поверхность П подшипника скольжения. Подшипник качения можно получить подобным же образом из груза Ц, передвигающегося на катках Д по плоскости П (фиг. 157), придав и в этом случае опорным поверхностям цилиндрические формы (фиг. 158). Так как коэффициент трения качения получается тем меньшим, чем тверже материалы тел качения (в подшипниках шариков или роликов) и деталей, по поверхностям которых перекатывание происходит, то поэтому, а также по некоторым другим соображениям подшип-Трение качения 145 ники качения изготовляются из твердых материалов в виде двух колец с шариками или роликами между ними. Для того чтобы расстояния между телами качения при
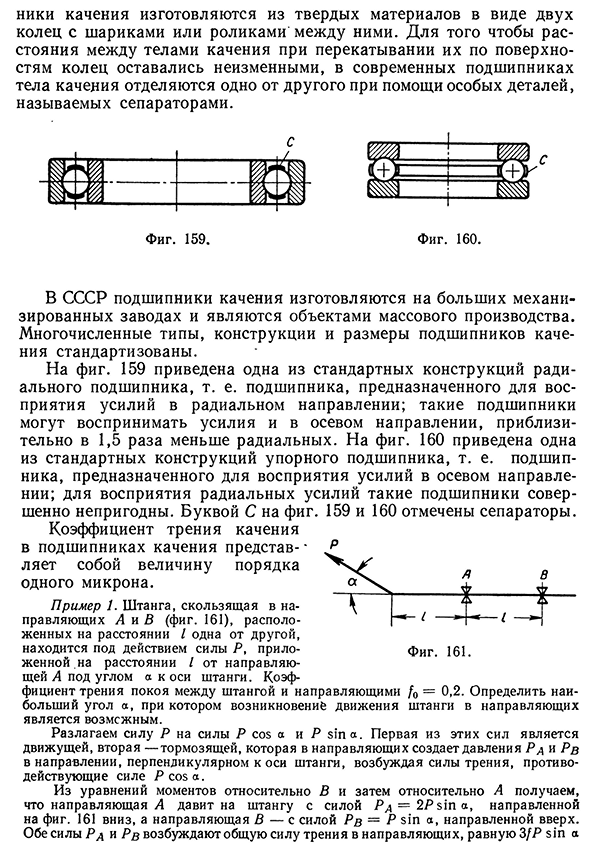
перекатывании их по поверхностям колец оставались неизменными, в современных подшипниках тела качения отделяются одно от другого при помощи особых деталей, называемых сепараторами. В СССР подшипники качения изготовляются на больших механизированных заводах и являются объектами массового производства. Многочисленные типы, конструкции и размеры подшипников качения стандартизованы. На фиг. 159 приведена одна из стандартных конструкций радиального подшипника, т. е. подшипника, предназначенного для восприятия усилий в радиальном направлении; такие подшипники могут воспринимать усилия и в осевом направлении, приблизительно в 1,5 раза меньше радиальных. На фиг. 160 приведена одна из стандартных конструкций упорного
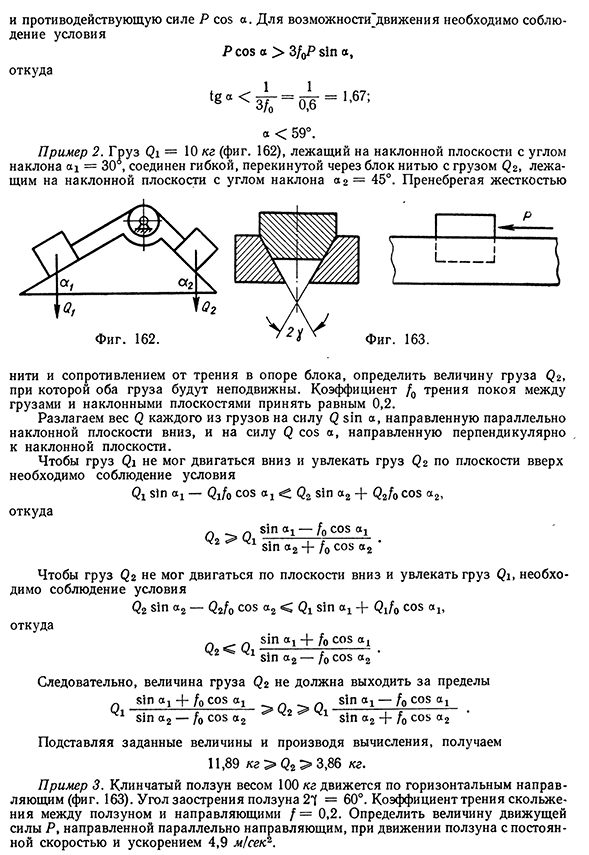
подшипника, т. е. подшипника, предназначенного для восприятия усилий в осевом направлении; для восприятия радиальных усилий такие подшипники совершенно непригодны. Буквой С на фиг. 159 и 160 отмечены сепараторы. Коэффициент трения качения в подшипниках качения представ ляет собой величину порядка одного микрона. Пример 1. Штанга, скользящая в направляющих А и В (фиг. 161), расположенных на расстоянии / одна от другой, находится под действием силы Р, приложенной. на расстоянии I от направляющей А под углом а к оси штанги. Коэффициент трения покоя между штангой и направляющими /0 = 0,2. Определить наибольший угол а, при котором возникновение движения штанги в направляющих является возможным. Разлагаем силу Р на силы Р cos а и Р sin а. Первая из этих сил является движущей, вторая —тормозящей, которая в направляющих создает давления Рд и Рв в направлении, перпендикулярном к оси штанги, возбуждая силы трения,
противодействующие силе P c o sa. Из уравнений моментов относительно В и затем относительно А получаем, что направляющая А давит на штангу с силой Рд = 2Psin а, направленной на фиг. 161 вниз, а направляющая В — с силой Рв = Р sin а, направленной вверх. Обе силы Рд и Рв возбуждают общую силу трения в направляющих, равную 3fP sin a 10 Зиновьев 612146 Трение в кинематических парах и противодействующую силе Р cos а. Для возможности’движения необходимо соблюдение условия Р cos а > 3/qP sin а, откуда а < 59°. Пример 2. Груз Qi = 10 кг (фиг. 162), лежащий на наклонной плоскости с углом наклона ах = 30°, соединен гибкой, перекинутой через блок нитью с грузом Q2, лежащим на наклонной плоскости с углом наклона а 2 = 45°. Пренебрегая жесткостью нити и сопротивлением от трения в опоре блока, определить величину груза Q2, при которой оба груза будут неподвижны. Коэффициент /0 трения покоя между
грузами и наклонными плоскостями принять равным 0,2. Разлагаем вес Q каждого из грузов на силу Q sin а, направленную параллельно наклонной плоскости вниз, и на силу Q cos а, направленную перпендикулярно к наклонной плоскости. Чтобы груз Qi не мог двигаться вниз и увлекать груз Q2 по плоскости вверх необходимо соблюдение условия QT sin ах — Qjfo cos 04 < Q2 sin a2 + Q2f0 cos a2, откуда Q2 > Q i S i n a i T V ° S a i • Sin a2 + 7o COS a2 Чтобы груз Q2 не мог двигаться по плоскости вниз и увлекать груз Qi, необходимо соблюдение условия Q2 sin a2 — Q2/0 cos a2 < Qi sin 04 + Q J0 cos 04, откуда Q2 < Q x s i n t t i + ^ C 0 S tti. 1 Sin a2 — /0 cos a2 Следовательно, величина груза Q2 не должна выходить за пределы sin «, + fo cos a, _ > Q sin ax — fo cos a, <1 sin a2 — f0 COS o2 V1 sin a2 + f0 COS a2 Подставляя заданные величины и производя вычисления, получаем 11,89 кг > Q2 > 3,86 кг. Пример 3. Клинчатый ползун весом 100 кг движется по горизонтальным направляющим (фиг. 163). Угол заострения ползун
а 27 = 60°. Коэффициент трения скольжения между ползуном и направляющими f — 0,2. Определить величину движущей силы Р, направленной параллельно направляющим, при движении ползуна с постоянной скоростью и ускорением 4,9 м/сек2.Примеры 147 Фиктивный коэффициент трения f f sin i sin 30 ° = 2/ = 0,4. Сила трения F = 100 кг-0,4 = 40 кг. Сила, необходимая для поддержания постоянной скорости движения, Р = F = 40 кг. Масса ползуна 1 0 0 2/ т — кг-сек^/м. У, о Сила, необходимая для движения ползуна с ускорением 4,9 м/сек?, Р = F + 4,9т = 40 + 4,9 т-з= 90 кг. 9,о Пример 4. Ведущее фрикционное колесо с диаметром Di = 300 мм (фиг. 164) и числом оборотов в минуту Л1 — 300 передает мощность N = 4 л. с. ведомому колесу с диаметром D 2 = = 450 мм. Коэффициент трения в месте соприкосновения ободов
колес f — 0,2. Валы, на которых насажены колеса, вращаются в подшипниках с диаметрами 40 мм. Коэффициент трения в опорах валов /1 = 0,08. Определить потери мощности от трения в опорах валов при колесах с цилиндрическими ободами и колесах с клинчатыми ободами. Угол заострения клинчатого обода 21 = 30° (фиг. 165). Угловая скорость вращения Фиг. 165. ведущего колеса При мощности N = 4 л. с. — 4-75 кем! сек = ЗШкгм/сек момент на валу ведущего колеса М — 300 кем)сек: 31,4 сек1 = 9,55 кем. Окружное усилие Р — 9,55 кем: М = 63,7 & 64 кг. Сила, с которой колеса должны быть прижаты одно к другому при цилиндри-ческих ободах, 10148 Трение в
кинематических парах Сила S, воспринимаемая опорами каждого из валов, является геометрической суммой двух слагающих: окружного усилия и силы Q. Так как линии действия этих £ил перпендикулярны одна к другой, то S = У/>2 + <22 = v 64а + 3202 = 326 кг. Сила трения в опорах каждого из валов равна S f — 326 кг −0,08 = 26 кг. Момент силы трения в опорах каждого из валов 520 кгмм кгм. Угловая скорость вращения ведомого вала Потери мощности на трение в опорах: ведущего вала 0,52 кал-31,4 сек1 = 16,3 кгм]сек\ ведомого вала 0,52 /сгл»-20,9 сек1 = 10,9 кгм/сек. При клинчатых ободах колес фиктивный коэффициент трения г = f f sin ч sin 15° = 3,8 4 /= 3,84-0,2 0,77. При таком коэффициенте трения необходимая сила нажатия Р 64 Q = Т = Q77 = 83,5 * 84 Сила, воспринимаемая опорами валов, S = у 642 + 842 = 106 кг
. Так как потеря мощности на трение в опорах вала пропорциональна силе S, то при клинчатых ободах потери мощности в опорах валов будут меньше, чем при цилиндрических ободах, в 326: 106 да 3 раза. П р и м е ч а н и е. Несмотря на вытекающее из приведенного выше сравнительного расчета преимущество фрикционных колес с клинчатыми ободами по сравнению с колесами с цилиндрическими ободами, фрикционная передача с клинчатыми колесами получила широкое применение лишь в приборах для передачи незначительной мощности, в силовых же передачах применяется редко. Дело в том,
что сопровождающееся износом относительное скольжение клинчатых ободов не может быть устранено: не скользят одна относительно другой лишь соприкасающиеся точки поверхностей ободов, лежащие на начальных окружностях. Пример 5. Детали А и В (фиг. 166) соединены болтом. Диаметр отверстия под болт немного (на 1–2 мм) больше диаметра болта. Наружный диаметр резьбы болта d = 20 мм, средний диаметр резьбы dcp = 18,4 мм, шаг резьбы s = 2,5 мм, угол при вершине профиля резьбы 2₽ = 60° (такая резьба предусмотрена ОСТ/НКТП 32).Примеры 149 Фиг. 166. пг в Болт затянут гаечным ключом силой Ро = 20 кг, приложенной к гаечному ключу на расстоянии I = 250 мм от оси болта. Коэффициент трения скольжения на всех поверхностях трения f = 0,2, коэффициент трения покоя /0 = 0,25. Равнодействующую элементарных сил трения на поверхности
соприкосновения гайки к детали А считать приложенной на окружности с диаметром D = 30 мм. Определить: 1) какой силой Т, направленной перпендикулярно к оси болта, можно сдвинуть детали А и В одну относительно другой и 2) какую силу надо приложить к гаечному ключу на расстоянии I от оси болта при демонтаже соединения. Сдвигу деталей А и В одной относительно другой препятствует сила трения на поверхности их соприкосновения. Сила трения, препятствующая сдвигу, равна Q/o, где Q — сила, сжимающая детали между гайкой и головкой болта. Производя давление на деталь А, затянутая гайка с такой же силой, но направленной в обратную сторону, растягивает болт. Болт затянут моментом М = = 20 кг-250 мм = ЬОШкгмм. В конце затягивания этот момент был уравновешен: 1) моментом Рг, где Р — сила на среднем радиусе
винтовой резьбы и г — средний радиус резьбы и 2) моментом QfR сил трения на поверхности соприкосновения гайки и дета ли А, где R — средний радиус, на котором приложена равнодействующая элементарных сил трения. Следовательно, Так как 5000 = 9,2Р + 3Q. Р = Q tg (А + <?’), то 5000 = Q [9,2 tg (Л + ? ’) + 3]. При шаге s = 2,5 мм и среднем диаметре резьбы dcp = 18,4 мм t g А л −18,4 * ° ’0 4 3, откуда Л = 2°30′. При /== 0,2 и угле 2? = 60° при вершине профиля резьбы фиктивный коэффи циент трения /’ = ■ I т= — 0 23 1 cosp 0,866 ″ u ’ d и соответствующий ему фиктивный угол трения < = arctg 0,23 = 13°00′. Следовательно, tg (А’ + т’) = tg (2°30′ + 13°) = 0,277; 5000 = Q (9,2-0,277 + 3) = 5,55Q, откуда Q = 5000: 5,55 = 900 кг,150 Трение в кинематических парах При /0 = 0,25 силу Т получаем равной Т = QfQ = 900-0,25 = 225 кг. При демонтаже соединения сила Ро, приложенная к ключу для
отвертывания гайки на расстоянии I = 250 мм от оси болта, создает момент Ро1, преодолевающий сопротивление: 1) момента Рг, где Р’ — сила на среднем радиусе г резьбы и 2) момента Qf R на поверхности соприкосновения гайки и детали А. В соответствии с формулой (10) где <р0 фиктивный угол трения покоя равен П = arctg f’Q = arctg А _ = arctg A g. = 16° 10′. Величина силы Р’ получается равной = 900 tg (16°10′ — 2°30′) = 218,7 ″ 219 кг. Следовательно, p ol = P ’r + Qfop , т. е. Pq-250 = 2199,2 + 900-0,25-15 = 5390 кгмм, откуда Ро = 5390: 2 5 0 # 21,6 кг. Пример 6. Определить, с какой силой надо действовать на рукоятку домкрата на расстоянии 800 лш от оси его винта (фиг. 167) для подъема груза весом 2000 кг с постоянной скоростью по следующим данным: 1) резьба винта трапецеидальная с углом при вершине профиля 2р = 30°, наружным диаметром d = 50 мм, средним диаметром dcp = 46 мм,
шагом s == 8 мм (резьба по ОСТ 2410); 2) коэффициент трения между винтом и гайкой f = 0,12; 3) коэффициент трения между головкой винта и не вращающейся головкой домкрата fi = 0,2; 4) диаметры кольцевой площади соприкосновения головок винта и домкрата: наружный D = 80 мм, внутренний Z)i=40 мм. Угол X подъема винтовой линии на среднем диаметре tg Л = — » 0,055; ndcp к • 46 Фиктивный коэффициент трения между винтом и гайкой f COS Р 0,12 cos 15° 0,124.Примеры 151 Фиктивный угол трения = arctg /’ — arctg 0,124 = 7°05′. Сила Р’, которую надо приложить на среднем радиусе винтовой резьбы для преодоления веса Q груза и силы трения в резьбе: Р’ = Q tg (X + / ) = 2000 tg (3° 10′ + 7°05′) = 360 кг. ; Момент ЛГ силы Р’ М’ = Р,( ^ = 360 к г ~ см = 828 кгсм. Сила F трения между головками винта и
домкрата ’ F = fv Q = 0,2-2000 = 400 кг (незначительный вес головки не принимается во внимание). Плечо L равнодействующей элементарных сил трения 2 + + 2 L ~ 3 2 (D -f-D l) 3 8 ^ + 8 −4 + 42 _ Х 2(8 + 4) 3,1 Момент М» силы F М» = 400 кг −3,1 см, — 1240 кгсм. Момент Л4, необходимый для подъема груза с постоянной скоростью: М = М’ + М» = 828 + 1240 = 2068 кгсм, Необходимая сила Ро на рукоятке р о = М: / = 2068: 80 = 25,85 ″ 26 Пример 7. Вертикальный вал В (фиг. 168), находящийся под действием силы Q = 400 кг, опирается вставленной в него кольцевой пятой П на неподвижную подушку /С подпятника. Пята вставлена в вал коническим хвостом с углом при вершине конуса 21 = 30°. Число оборотов вала в минуту покоя на поверхности соприкосновения пяты и вала /0 = 0,2; коэффициент трения
скольжения между пятой и подушкой f — 0,08. Размеры поверхностей соприкосновения указаны на фиг. 168. Определить потерю мощности на трение и выяснить, возможно ли при вращении вала вращение пяты относительно вала. Сила трения на поверхности соприкосновения пяты и подушки п — 300. Коэффициент трения Плечо Я силы трения Qf = 400-0,08 = 32 кг. 302 + 30-10+ 102 3 0 + 10 = 21,7 ″ 22 мм. Момент силы трения Mf = 32 кг-22 мм = 704 кгмм & 0,7 кгм. Угловая скорость вращения вала тс-п сек-152 Трение в кинематических парах Потеря мощности на трение М р и — 0,7 кал-31,4 сек1 = 21,98 & 22 кем/сек. Фиктивный коэффициент трения покоя на поверхности соприкосновения пяты и вала /о = /о: sin 1 = 0,2: sin 15° 0,77. Сила трения на поверхности соприкосновения пяты и вала QfQ = 400 кг −0,77 = 308 г. При равномерном распределении
элементарных сил трения по высоте поверхности соприкосновения пяты и вала (что можно предположить при достаточно точной обработке поверхностей сплошного и полого усеченных конусов) равнодействующую элементарных сил трения можно считать приложенной на одинаковом расстоянии от большого и малого оснований конической поверхности соприкосновения, т. е. при высоте этой поверхности, равной 20 мм на расстоянии 10 мм от нижнего основания. Радиус окружностей нижнего основания равен 25: 2 = 12,5 мм\ на высоте IOjwjw от нижнего основания радиус поперечного сечения равен 12,5 — 10 tg 15° = 9,9 мм. Необходимый для вращения пяты относительно вала момент, равный 308 кг −9,9 мм
= 2999 кгмм & 3 кгм, превышает момент M j = 0,7 кгм сил трения на поверхности соприкосновения пяты и подушки в 3: 0,7 = 4,3 раза. Следовательно, возможность вращения пяты относительно вала исключена. Пример 8. Гибкое тело огибает три неподвижных цилиндра, как показано на фиг. 169. На одном конце гибкого тела подвешен груз Qi = 100 кг. Определить, при какой величине груза Q2, подвешенного на другом конце гибкого тела, оба груза будут неподвижны. Коэффициент трения между гибким телом и цилиндрами f = 0,32. Общий угол охвата гибким телом всех цилиндров равен 3-гс. Приняв показатель степени в формуле Эйлера равным fa = 0,32.3-гс » 3, получаем условия для невозможности движения вниз груза QxCQa^3; » Q2 Qi3. Следовательно, величина груза Q2 должна находиться в пределах < Qs < Qie3. Приняв е3 = 2,728 & 20, получаем 5 кг < Q2 < 2000 кг.
Смотрите также:
| Трение скольжения смазанных тел | Коэффициент полезного действия |
| Трение гибких тел | Уравнение движения машины |

